27-02-2025 - Analytic Geometry - Degenerate Conic [EN]-[IT]

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

ENGLISH
27-02-2025 - Analytic Geometry - Degenerate Conic [EN]-[IT]
With this post I would like to give a brief instruction about the topic mentioned in the subject
(code notes: X_58)

Degenerate Conic
First of all let's start by defining what a conic is.
A conic is an algebraic of degree two.
In analytical geometry a degenerate conic does not represent a curve as we are led to imagine. It is not an ellipse or a parabola, but it is a figure composed of two lines.
Formal definition
A conic is represented by a quadratic equation in two variables, this equation is expressed below.

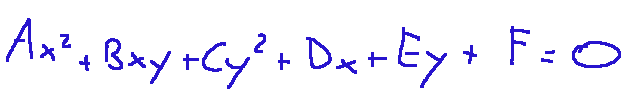
Simpler definition
We can also say that a degenerate conic is such when the discriminant of the conic does not describe a classical curve, but describes:
-A pair of lines (inciding or coinciding)
-A single point (when two lines coincide at a point)

Examples of conics degenerates

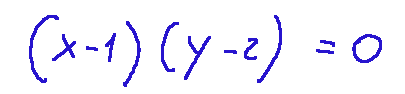
This equation represents two distinct lines that intersect, the line x=1 and y=2

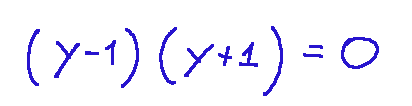
This equation instead represents two parallel lines y=1 and y=-1

Exercise
Let's try the following exercise. I won't go into details so as not to make the writing too heavy, so some basic knowledge is necessary to fully understand the exercise.
The exercise deals with a problem of projective geometry regarding degenerate conics.
Let's take these 4 degenerate conics

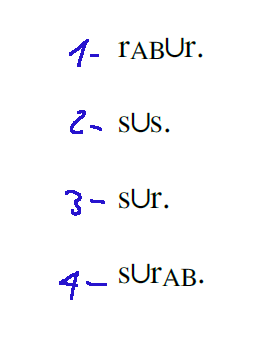
Which of these conics is a degenerate conic of the bundle of conics that contain the two points A and B and are tangent to the line s at point A and to the line r at point B, indicated in the figure?

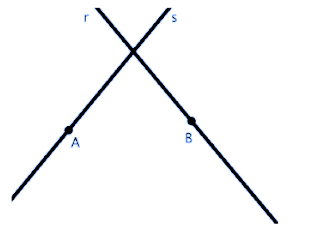
Let's analyze the situation
We need to identify which of the given conics is degenerate and belongs to the bundle of conics that:
-Pass through the points A and B
-Are tangent to the line s in A and to the line r in B.

At this point we can deduce that the correct degenerate conic will be formed by the union of the lines s and r because:
-The line s passes through A and is tangent at that point
-The line r passes through B and is tangent at that point.

Solution
The degenerate conic required is given by the union of the lines s and r. If we analyze the probable solutions given at the beginning we can say that the correct answer is the third one, that is:

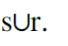
Conclusions
In analytical geometry, or more precisely in projective geometry, a degenerate conic is represented by the union of two lines and these lines can be tangent at certain points or can pass through certain points.

Question
Have you ever done any exercises on degenerate conics? Is this the first time you've heard of degenerate conics?

[ITALIAN]
27-02-2025 - Geometria analitica - Conica degenere [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_58)

Conica degenere
Innanzitutto iniziamo con i definire che cosa è una conica.
Una conica è una algebriche di grado due.
In geometria analitica una conica degenere non rappresenta una curva come siamo portati ad immaginare. Essa non è un ellisse o una parabola, ma è una figura composta da due rette.
Definizione formale
Una conica è rappresentata da un equazione quadratica in due variabili, qui di seguito è espressa questa equazione.

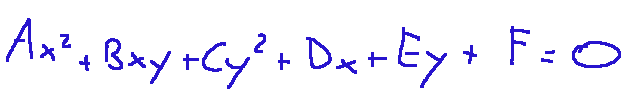
Definizione più semplice
Possiamo dire anche che una conica degenere è tale quando il discriminante della conica non descrive una curva classica, ma descrive:
-Una coppia di rette (incidenti o coincidenti)
-Un punto singolo (quando due rette coincidono in un punto)

Esempi di coniche degeneri

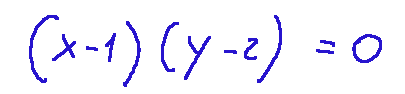
Questa equazione rappresenta due rette distinte che si intersecano, la retta x=1 e y=2

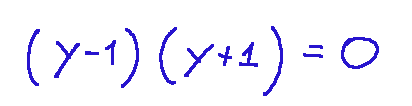
Questa equazione invece rappresenta due rette parallele y=1 e y=-1

Esercizio
Proviamo ad eseguire il seguente esercizio. Non entrerò nei dettagli per non appesantire troppo la scrittura, quindi alcune conoscenze di base sono necessarie per comprendere fino in fondo l'esercizio.
L'esercizio tratta di un problema di geometria proiettiva riguardante le coniche degeneri.
Prendiamo queste 4 coniche degeneri

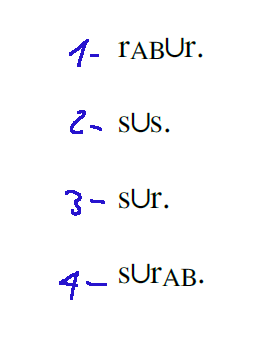
Quale di queste coniche è una conica degenere del fascio di coniche che contengono i due punti A e B e sono tangenti alla retta s nel punto A e alla retta r nel punto B, indicati in figura?

Analizziamo la situazione
Dobbiamo individuare quale tra le coniche date è degenere e appartiene al fascio di coniche che:
-Passano per i punti A e B
-Sono tangenti alla retta s in A e alla retta r in B.

A questo punto possiamo dedurre che la conica degenere corretta sarà formata dall'unione delle rette s e r perché:
-La retta s passa per A ed è tangente in quel punto
-La retta r passa per B ed è tangente in quel punto.

Soluzione
La conica degenere richiesta è data dall'unione delle rette s e r. Se andiamo ad analizzare le probabili soluzioni date in partenza possiamo dire che la risposta corretta è la terza, cioè:

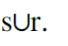
Conclusioni
In geometria analitica, o più precisamente nella geometria proiettiva, una conica degenere è rappresentata dall'unione di due rette e queste rette possono essere tangenti in certi punti oppure possono passare per certi punti.

Domanda
Avete mai fatto qualche esercizio sulle coniche degeneri? E' la prima volta che sentite parlare di coniche degeneri?

THE END