25-02-2025- Analytic Geometry - Homogeneous Implicit Form [EN]-[IT]

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

ENGLISH
25-02-2025- Analytic Geometry - Homogeneous Implicit Form [EN]-[IT]
With this post I would like to give a short instruction about the topic mentioned in the subject
(code notes: X_59)

Homogeneous Implicit Form
Let's start by saying that algebraic curves in the plane are the natural generalization of straight lines, and are obtained by increasing the degree
of the polynomials that define them.

Homogeneous Implicit Form of a Tangent Line to an Algebraic Curve
So now let's clarify what a homogeneous implicit form of a tangent line to an algebraic curve is.
This is an equation that describes the tangent line in terms of homogeneous coordinates.
Homogeneous coordinates are used in projective geometry.

Exercise
Let's consider these 4 homogeneous implicit forms:

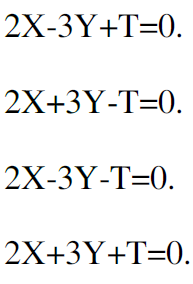
Which of the previous ones is a homogeneous implicit form of the tangent line to the algebraic curve with homogeneous equation X4-3Y2T2+2T4=0 at the point [1 1 1] in the
plane?

Below are the steps. I will not go into detail on some of these so as not to make the solution too long.

Let's start by finding the tangent line to the algebraic curve

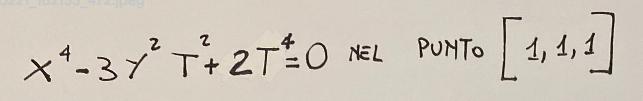
Let's focus on our starting point which is the algebraic curve

Now let's calculate the gradient. Let's try to understand what is the gradient of the curve that is the vector of the partial derivatives with respect to X, Y, and T:

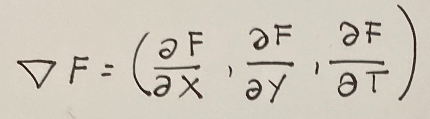
The partial derivatives will then be as follows.

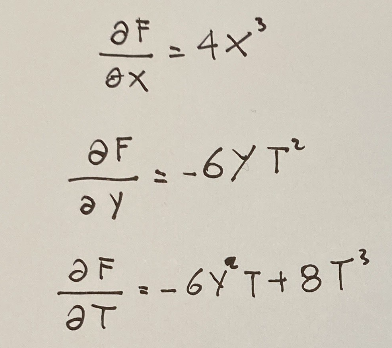
Evaluation of the gradient
Let's now move on to the evaluation of the gradient at the point [1,1,1]
At this point we make the substitutions:
X = 1
Y = 1
T = 1
in the partial derivatives.
In order not to go into too much detail, I will show the simplest one, which is that of X. Here it is below:

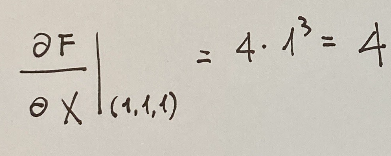
Tangent line
After calculating the partial derivatives, we move on to forming the equation in the tangent line.
The tangent line to the curve at point [1,1,1] is given by:

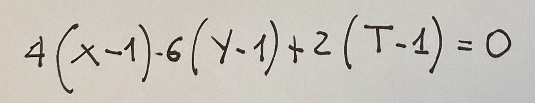
Continuing with the development of these calculations we will obtain the following, that is, the following simplification of the equation:

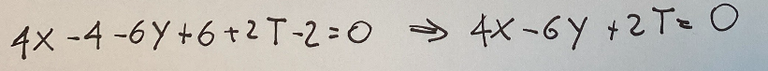
Dividing everything by 2 we obtain a simpler form, the one below shown

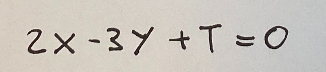
Result
So, the tangent line to the algebraic curve at the point [1,1,1] is given by the equation 2X - 3Y + T = 0

Conclusions
The homogeneous implicit forms of a tangent line to an algebraic curve are used in projective geometry and are calculations that are mainly used in cartography.

Question
Did you know that these calculations, which at first glance may seem rather complex, are fundamental to improving the precision of maps and geodetic measurements?

[ITALIAN]
25-02-2025 - Geometria analitica - Forma implicita omogenea [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_59)

Forma implicita omogenea
Iniziamo con il dire che le curve algebriche nel piano sono la naturale generalizzazione delle rette, e sono ottenute aumentando il grado
dei polinomi che le definiscono.

Forma implicita omogenea di una retta tangente ad una curva algebrica
Quindi ora chiariamo che cosa è una forma implicita omogenea di una retta tangente ad una curva algebrica.
Questa è un'equazione che descrive la retta tangente in termini di coordinate omogenee.
Le coordinate omogenee sono utilizzate in geometria proiettiva.

Esercizio
Prendiamo in considerazione queste 4 forme implicite omogenee:

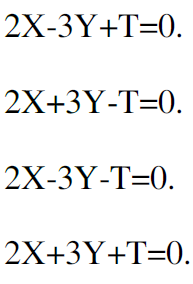
Quale delle precedenti è una forma implicita omogenea della retta tangente alla curva algebrica con equazione omogenea X4-3Y2T2+2T4=0 nel punto [1 1 1] nel
piano?

Qui di seguito i passaggi. Su alcuni di questi non entrerò nel dettaglio per non rendere troppo lungo lo svolgimento.

Partiamo per trovare la retta tangente alla curva algebrica

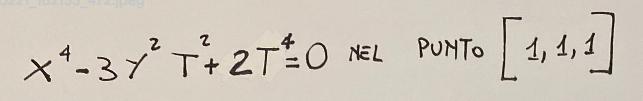
Focalizziamo il nostro punto dipartenza che è la curva algebrica

calcoliamo ora il gradiente. Cerchiamo di capire quel è il gradiente della curva che è il vettore delle derivate parziali rispetto a X,Y, e T:

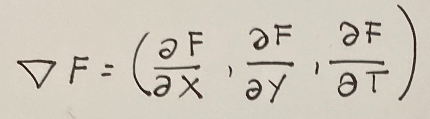
Le derivate parziali risulteranno quindi come di seguito.

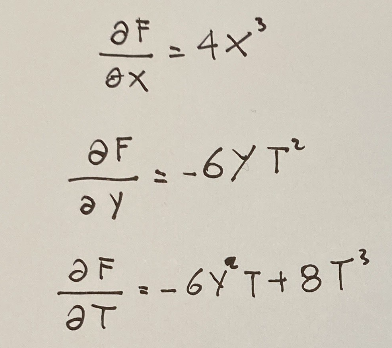
Valutazione del gradiente
Passiamo ora alla valutazione del gradiente nel punto [1,1,1]
A questo punto effettuiamo le sostituzioni:
X = 1
Y = 1
T = 1
nelle derivate parziali.
Per non dilungarmi troppo mostrerò la più semplice che è quella di X. Eccola qui di seguito:

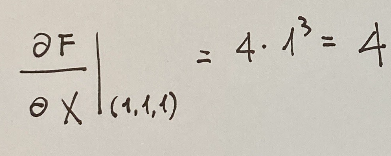
Retta tangente
Dopo aver calcolato le derivate parziali passiamo alla formazione dell'equazione nella retta tangente.
La retta tangente alla curva nel punto [1,1,1] è data da:

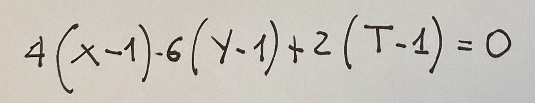
Proseguendo con lo sviluppo di questi calcoli otterremo quanto segue, cioè la seguente semplificazione dell'equazione:

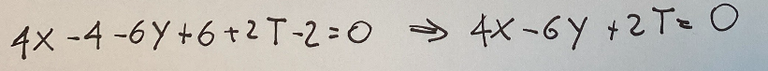
Andando a dividere tutto x 2 otteniamo una forma più semplice, quella qui di seguito mostrata

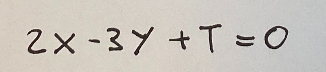
Risultato
Quindi, la retta tangente alla curva algebrica nel punto [1,1,1] è data dall'equazione 2X - 3Y + T = 0

Conclusioni
Le forme implicite omogenea di una retta tangente ad una curva algebrica vengono usate nella geometria proiettiva e sono calcoli che vengono soprattutto usati nella cartografia.

Domanda
Lo sapevate che questi calcoli, che a prima vista potrebbero essere piuttosto complessi, sono fondamentali per migliorare la precisione delle mappe e delle misure geodetiche?

THE END