05-02-2025 - Analytic Geometry - The determinant of a matrix [EN]-[IT]

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

ENGLISH
05-02-2025 - Analytic Geometry - The determinant of a matrix [EN]-[IT]
With this post I would like to give a short instruction about the topic mentioned in the subject
(code notes: X_84)

The determinant of a matrix
The determinant of a square matrix is ​​a number that provides information about the properties of the matrix.
That is:
If the determinant of a matrix is ​​different from zero, it means that the matrix is ​​invertible
If the determinant of a matrix is ​​equal to zero, it means that the matrix is ​​not invertible and is also called singular.

The calculation of the determinant of a 2x2 matrix is ​​simple and is calculated as follows:
Matrix A

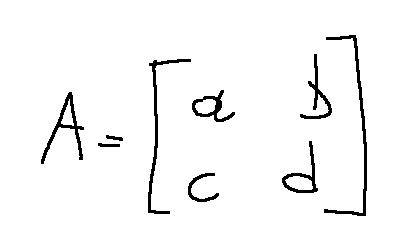
I identify the diagonals

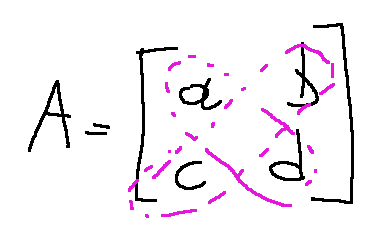
The determinant is calculated with the following formula

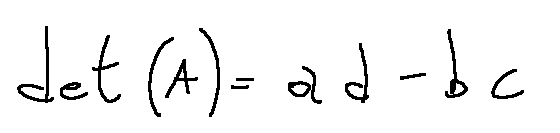
Example with 4 x 4 matrix
I will not explain all the steps, but I will perform the main phases
Let's take the following matrix as an example

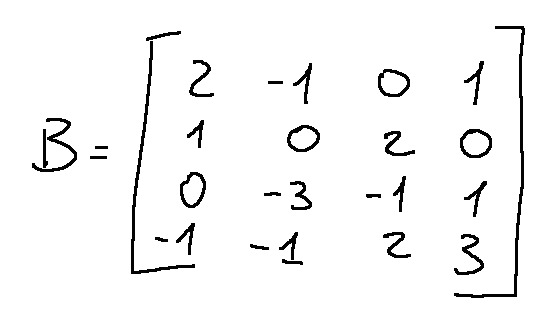
To calculate the determinant we can use the expansion of Laplace

Step 1
Laplace expansion with respect to the first row
To expand the determinant we use the first row

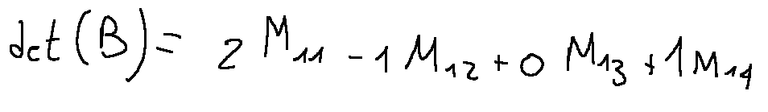
NOTE: Mij is the minor obtained by eliminating the i-th row and the j-th column

Step 2
Calculating minors
M11 eliminating the first row and the first column will be shown so

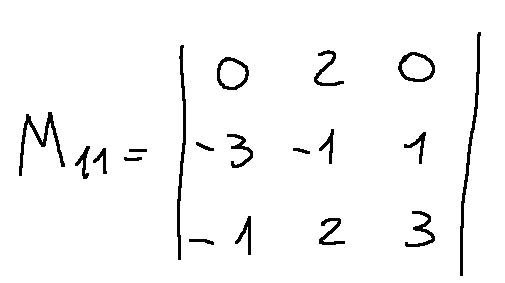
The calculation of the determinant would be next

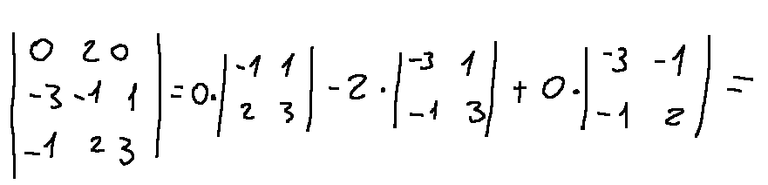
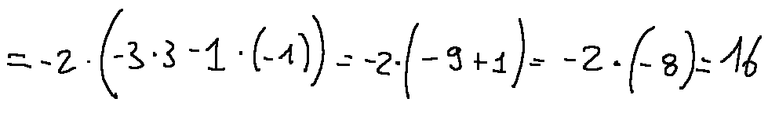
At this point I follow the same procedure for M12 and M14
I get M12 by eliminating the first row and the second column
I will have that M12 = -7
M14 I will get by eliminating the first row and the fourth column
I will have that M14 = -13

Step 3
I intervene in the calculation of the determinant with the substitution in the formula and I will get this

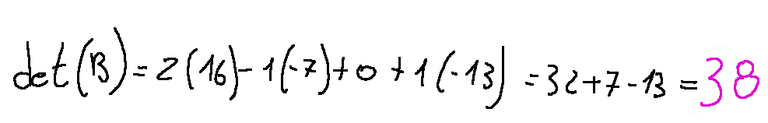
So, the determinant of the matrix taken as an example is 38.

Conclusions
To calculate the determinant of a 2x2 matrix we have the diagonal rule, to calculate a 3x3 matrix we use the Sarrus rule and for nxn matrices (with n>=4) we use the Laplace expansion

Question
Have you ever tried to calculate the determinant of a matrix? Do you remember studying matrices at school?

[ITALIAN]
05-02-2025 - Geometria analitica - Il determinante di una matrice [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_84)

Il determinante di una matrice
Il determinante di una matrice quadrata è un numero che fornisce informazioni sulle proprietà della matrice.
Cioè:
Se il determinante di una matrice è diverso da zero vuol dire che la matrice è invertibile
Se il determinante di una matrice è uguale a zero vuol dire che la matrice non è invertibile ed è detta anche singolare.

Il calcolo del determinante di una matrice 2x2 è semplice e si calcola come segue:
Matrice A

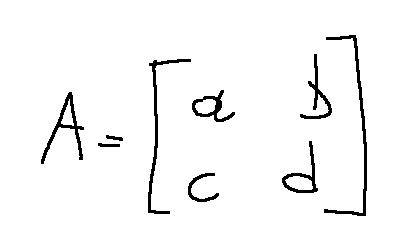
Individuo le diagonali

Il determinante si calcola con la seguente formula

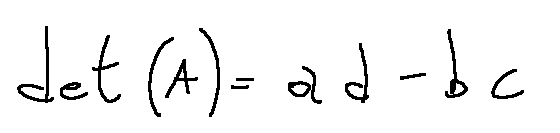
Esempio con matrice 4 x 4
Non spiegherò tutti i passaggi, ma eseguirò le fasi principali
Prendiamo come esempio la seguente matrice

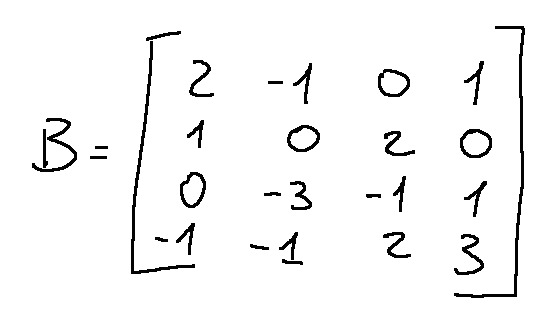
Per calcolare il determinante possiamo usare l'espansione di Laplace

Passaggio 1
Espansione di Laplace rispetto alla prima riga
Per espandere il determinante usiamo la prima riga

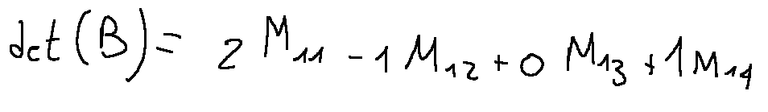
NOTA: Mij è il minore ottenuto eliminando la i-esima riga e la j-esima colonna

Passaggio 2
Calcolo dei minori
M11 eliminando la prima riga e la prima colonna si mostrerà così

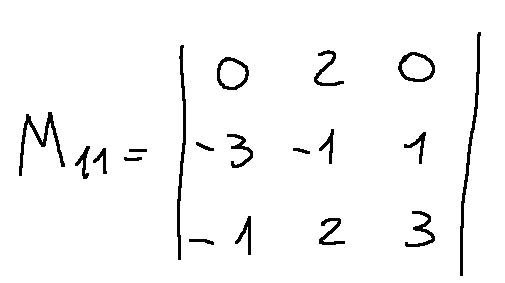
Il calcolo del determinante sarebbe il seguente

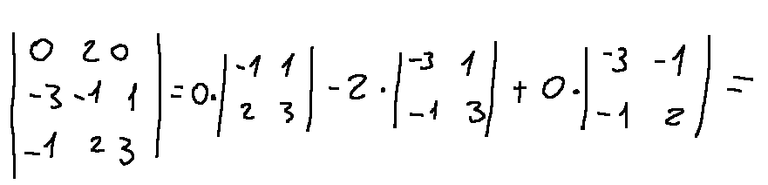
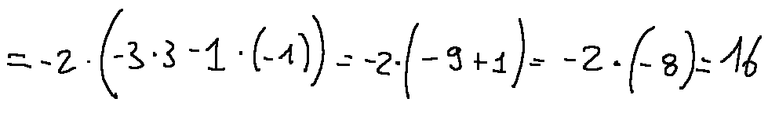
A questo punto seguo lo stesso procedimento per M12 e M14
M12 la ottengo eliminando la prima riga e la seconda colonna
Avrò che M12 = -7
M14 la otterrò eliminando la prima riga e la quarta colonna
Avrò che M14 = -13

Passaggio 3
Intervengo nel calcolo del determinante con la sostituzione nella formula e otterrò questo

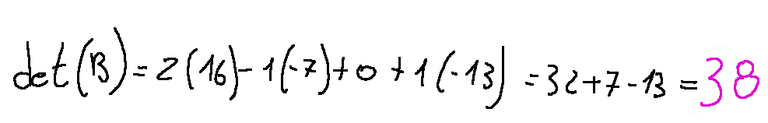
Quindi, il determinante della matrice presa come esempio è 38.

Conclusioni
Per calcolare il determinante di una matrice 2x2 abbiamo la regola delle diagonali, per calcolare una matrice 3x3 usiamo la regola di Sarrus e per matrici nxn (con n>=4) usiamo l'espansione di Laplace

Domanda
Avete mai provato a scuola a calcolare il determinante di una matrice? Vi ricordate di aver studiato a scuola le matrici?

THE END