03-11-2024 - Analytic Geometry - Matrix Multiplication [EN]-[IT]

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

ENGLISH
03-11-2024 - Analytic Geometry - Matrix Multiplication [EN]-[IT]
With this post I would like to give a short instruction about the topic mentioned in the subject
(code notes: X_086)

Matrix Multiplication
Matrix multiplication may seem complicated at first sight, but if well understood, it is not so difficult to perform.

Suppose we want to multiply two square matrices A and B, how will our matrix C be the source of the product of A x B?

Let's write two matrices in which the elements do not appear as numbers but as indicative elements of the matrices.

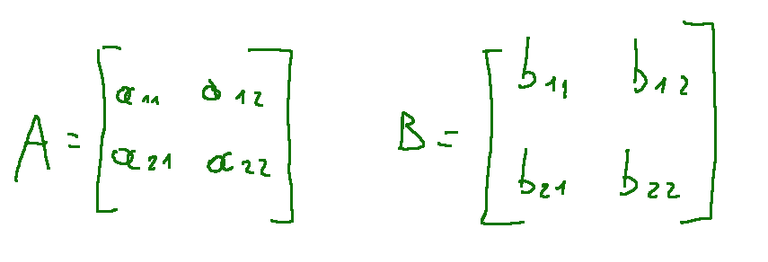
The multiplication between them will give rise to a C matrix

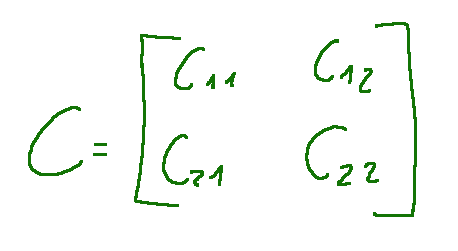
Here, now we have to understand how we have to get c11, c12, c21 and c22.

Below are the calculations explained.

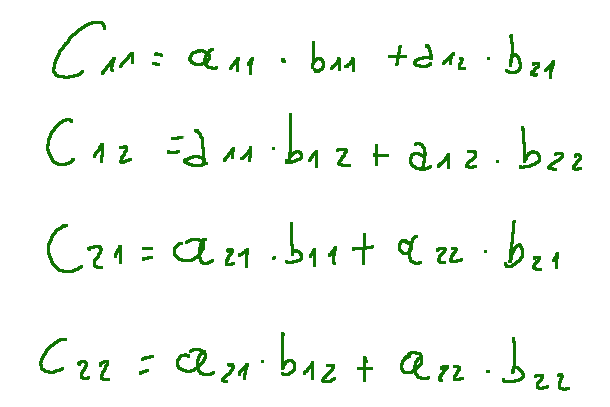
Below I explain graphically how to calculate c11

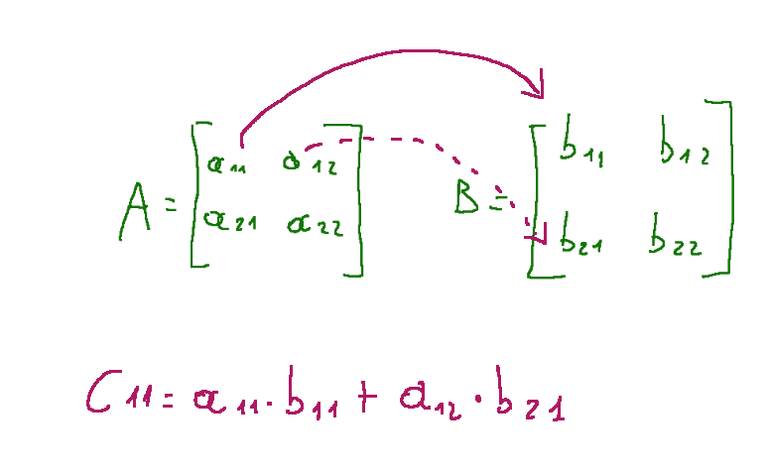
Below I explain graphically how to calculate c12

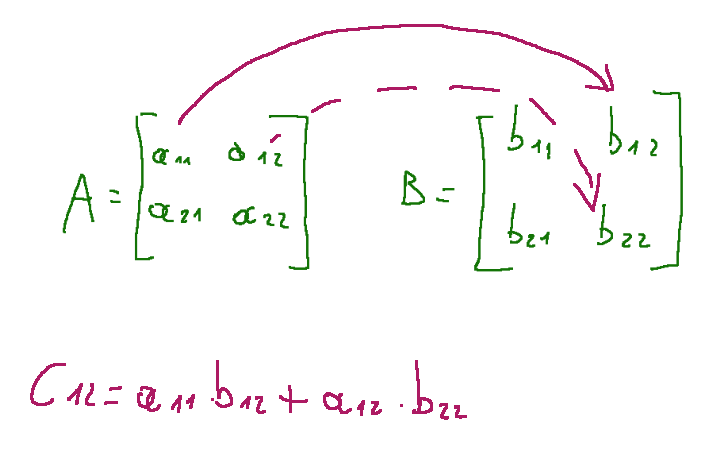
Below I explain graphically how to calculate c21

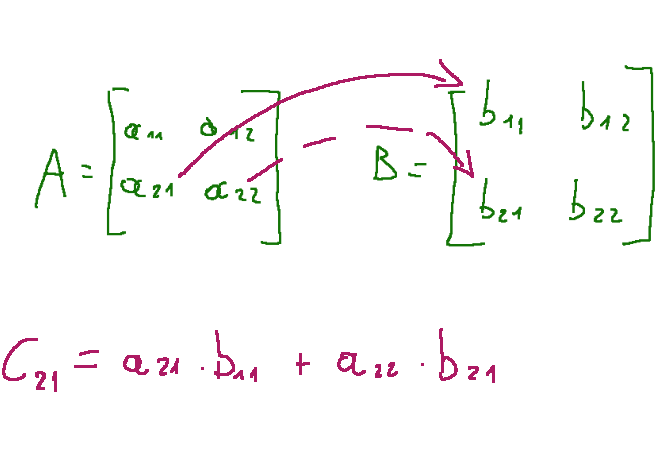
Below I explain graphically how to calculate c22

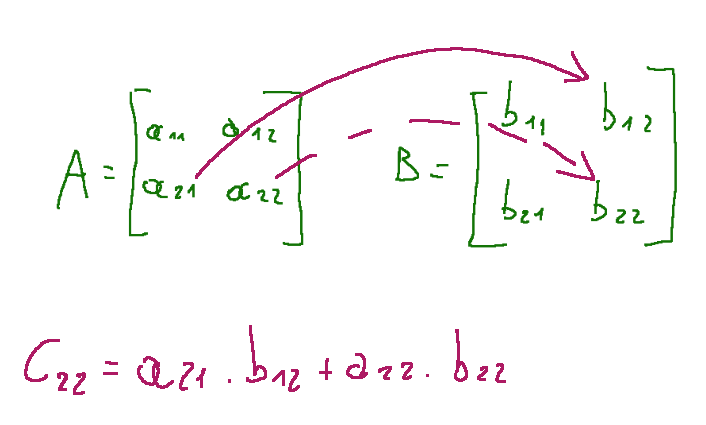
Conclusions
Matrix multiplication follows the following rule. Each element of the resulting matrix is ​​obtained as the sum of the products between the elements of the row of the first matrix and the elements of the column of the second matrix

Question
Matrix multiplications seem much more difficult to understand than sums, what do you think?

---

---

[ITALIAN]
03-11-2024 - Geometria analitica - Moltiplicazione di matrici [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_086)

Moltiplicazione di matrici
La moltiplicazione tra matrici può risultare a prima vista complicata, ma se ben compresa, non è così difficile da eseguire.

Supponiamo di voler moltiplicare due matrici quadrate A e B, come sarà la nostra matrice C fonte del prodotto di A x B?

Scriviamo due matrici in cui gli elementi non appaiono come numeri come come elementi indicativi delle matrici.

La moltiplicazione tra esse darà origine ad una matrice C

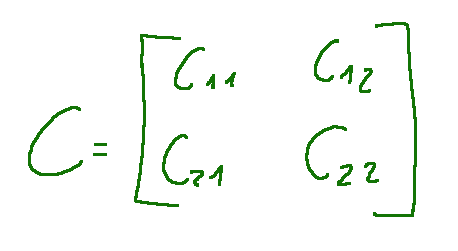
Ecco, ora dobbiamo capire come dobbiamo fare a ricavare c11, c12, c21 e c22.

Qui di seguito sono spiegati i calcoli.

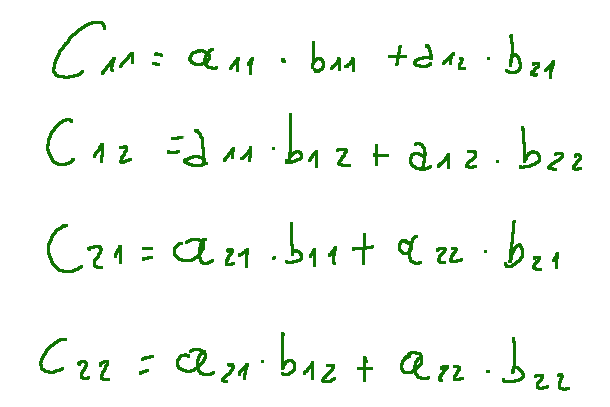
Qui di seguito spiego graficamente come si calcola c11

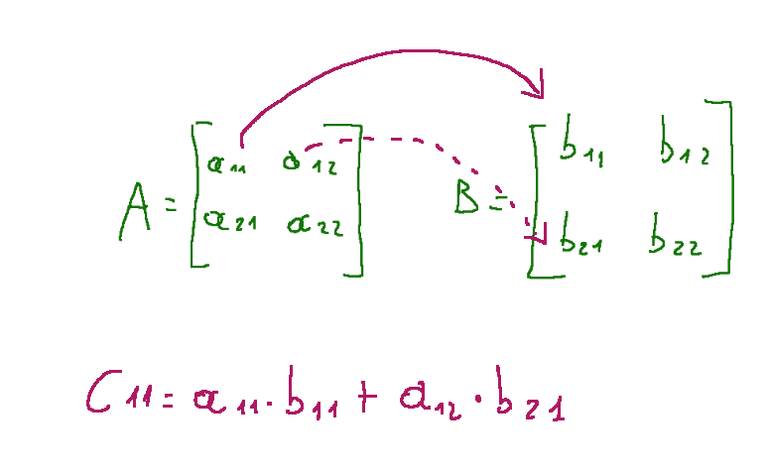
Qui di seguito spiego graficamente come si calcola c12

Qui di seguito spiego graficamente come si calcola c21

Qui di seguito spiego graficamente come si calcola c22

Conclusioni
La moltiplicazione tra matrici segue la seguente regola. Ogni elemento della matrice risultante si ottiene come somma dei prodotti tra gli elementi della riga della prima matrice e gli elementi della colonna della seconda matrice

Domanda
Le moltiplicazioni tra matrici mi sembrano molto più difficili da comprendere rispetto alle somme, voi che ne pensate?

THE END