Hi Everyone,

Welcome to the second post in my conference and journal paper post series. This series will contain ten conference and journal papers from my time working in the Queensland Government. In my post, My Peer Reviewed Conference and Journal Papers, I explain the purpose of this series.

Proposed Modifications to the Cost-Benefit Analysis Decision Criteria for Road Project Evaluation to Improve Decision-making was the first paper I worked on when I joined Transport and Main Roads. I wanted to present it at the 2010 ARRB Conference. However, the paper was rejected. The initial version of the paper was not that strong and was overaggressive in its criticism of existing decision criteria. I referred to the criteria, which consisted of the benefit cost ratio, net present value, and first year rate of return, as the three stooges. Considering this was the held standard at the time, it did not go down well with economists involved in the conference. To make matters worse, the economist who reviewed the paper wrote the guidelines advocating for this decision criteria.

After rejection, I put the paper to one side. Instead, I went to work on the flooding paper. Around a year later, I went back to work on the paper. At this point, my skills in writing papers had improved. I made many changes to the initial paper. The paper was considerably better than before. I submitted it to the Transportation Journal. This led to a long wait. Eventually, they got back to me to inform me. They informed me that the paper had been accepted but as an industry note rather than a full article. They required me to reduce the content to around 4,000 words. This was not too difficult to do. I did so by removing sections relating to project timing. This did not change the main gist of the paper. The paper was accepted again and was published in the third quarter of 2012.

I consider this paper to be significant because it challenged the flawed economic decision criteria that was being used to prioritise projects. This paper also fed into my later work relating to assessing programs. I use the criteria outlined in this paper to rank projects within programs. This eventually led to me running into problems with senior management in Transport and Main Roads. However, at this point the department was still supportive of my papers and research.

This post contains the full version of the paper, which is a few thousand words longer than the one published in the Transportation Journal.

Proposed Changes to the Cost Benefit Analysis Decision Criteria for Road Projects¹

---

Abstract

---

The Australian Transport Council (ATC) have identified that the benefit cost ratio (BCR), the net present value (NPV) and first year rate of return (FYRR) decision criteria are appropriate inputs to project prioritization, mutual exclusive project selection and optimal timing respectively. This paper suggests the net benefit investment ratio (NBIR), the incremental net benefit investment ratio (INBIR) and the internal rate of return (IRR) subject to decision criteria incorporating the marginal project as alternatives to those proposed by the ATC. The proposed decision criteria aim to reduce the impact of uncertainty surrounding discount rates and opportunity costs of capital, hence improving the quality of the quantitative inputs provided to decision makers.

1. Introduction

---

Billions of dollars a year are invested in road infrastructure in Australia. There are innumerable ways of spending this money to improve the road networks. Decision rules are established to determine, which projects are economically viable. Most of these rules are subject to the premise that resources are efficiently allocated to road infrastructure and the discount rate is representative of the opportunity costs of the proposed projects. In reality, this is rarely the case, imperfect information and inflexibility of resource allocation results in either the underfunding or overfunding of sectors of the economy (Arrow 1974) and discount rates fluctuate widely depending on the methodology applied to derive them (Baumol 1968 and Weitzman 2001).

The three economic measures that are currently recommended by the Australian Transport Council (ATC) are the benefit cost ratio (BCR), the net present value (NPV) and the first year rate of return (FYRR). The BCR is an input to project prioritization, the NPV is applied to mutually exclusive project selection and the FYRR is used to estimate optimal project timing. This paper identifies the problems in consistency of selecting mutually exclusive projects based on the NPV while applying the BCR to project prioritization. The application of the net benefit investment ratio (NBIR) as an input to project prioritization and the application of the incremental net benefit investment ratio (INBIR) to mutually exclusive project selection measured against the NBIR of the marginal project are proposed alternatives to remedy these problems. The incompleteness of the FYRR as an adequate indicator of optimal project timing is raised and compared with the internal rate of return (IRR) as a proposed alternative.

2. The Influence of Discount Rates on Decision Criteria

---

Conventional decision criteria suggest that projects are rejected or accepted on economic grounds if the project improves quantifiable social welfare. Examples of such criteria are as follows: NPV>0, BCR>1 and IRR>r² . All these criteria are subject to the reliability of the discount rate. Ross (1995) suggests that the viability of projects could change in a matter of months as bond rates tend to fluctuate, thus increasing the difficulty of selecting a representative discount rate. Weitzman (1998) argues that discount rates should be decreased to the lowest possible rate as the life of projects approach infinity. Weitzman (2001) introduces the concept of Gamma discounting³ . He argues that the wide distribution of predictions of the real-interest-rate by economists implies that discount rates are more uncertain than the returns to a project, therefore, justifying a decreasing discount rate. Infrastructure Australia has prescribed three different discount rates of 4, 7 and 10 per cent (Australian Government 2008). Different discount rates could change the reported economic viability of some projects if the conventional decision criteria are strictly adhered too.

Justifying projects based on decision criteria heavily dependent on discount rates, which may vary depending on the timing of the selection of the bond rate and methodology applied to determining the discount rate (Baumol 1968), may not be the most effective method of justifying projects. Baumol (1969) states that the discount rate for Government projects should be equivalent to the rate of return the resources utilized would otherwise provide in the private sector. If we consider the opportunity cost of a road infrastructure project to be that of another road infrastructure project rather than a private sector project, the long run bond rate may not be the most appropriate discount rate. Booz Allen Hamilton (2007) suggested the social opportunity costs of capital could be used as an alternative to the bond rate as a discount rate. The social opportunity cost is derived from the return of an alternative project. The selection of the alternative project was deemed as an impeding limitation to this method. This paper will briefly discuss a possible method of applying the social opportunity cost of capital approach by proposing that the marginal project fulfils the role of the above-mentioned alternative project. Another possible solution would be to apply decision criteria to project evaluation that is less dependent on the discount rate; such a method would be to compare evaluated projects with each other rather than a standard numerical criteria.

3. Benefit Cost Ratio

---

The benefit cost ratio (BCR) has become the primary tool applied to project prioritization in Australia. The BCR by definition is the ratio of the present value of economic benefits to the present value of economic costs of a proposed initiative (ATC 2006a). In the context of a road project, costs could be split into maintenance, rehabilitation and capital costs (Austroads 1996). These costs could be incurred over a number of periods; maintenance is likely to be incurred every year of the project’s life. While rehabilitation is less frequent, it is likely to be incurred during the latter periods of the project’s life (DTMR 2011).

Investments in projects should be economically justified based on the returns to the investment, i.e. the capital (Pace 2003), as the efficiency of capital is subject to evaluation rather than the costs for the entire life of the project (Campbell and Brown 2003). The BCR demonstrates a relationship between benefits and costs, not a relationship between benefits and capital. Prioritizing projects based on a BCR involves prioritizing projects based on future expenditure and not just on the current capital expenditure of the project. The prioritization process for projects with high maintenance costs could be distorted by prioritizing with the BCR.

The ATC (2006a) proposed an alternative BCR formula. The change would involve shifting the maintenance and rehabilitation costs, which were previously in the denominator of the BCR formula, to the numerator of the formula. For simplicity, we will call the ATC BCR formula, the BCR_ATC, this formula is given in Equation 2 and the traditional BCR formula is given in Equation 1.

Equation 1: BCR

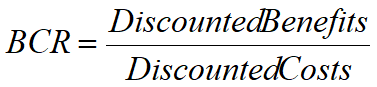
Equation 2: ATC version of BCR⁴

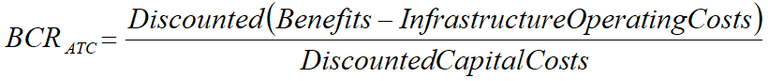
The BCR_ATC formula expresses benefits as a ratio to capital expenditure. Projects can be ranked based on this new formula without the distortions of infrastructure operating costs. The problem with the BCR formula proposed by the ATC is that this formula is the formula for the net benefit investment ratio (NBIR) (Campbell and Brown 2003 and Perkins 1994). The ATC guidelines acknowledge that the proposed formula is the NBIR but proposes that the BCR applied to road projects should have the same formula as the NBIR. The reason given by the ATC for the use of the name BCR, is that the BCR is a well known economic measure and has a definition often quoted the same as the NBIR (ATC 2006c).

Redefining the BCR formula could produce more problems than it solves. Firstly, the uptake of the new BCR formula has not been universal throughout Australia. RTA (2006), Austroads (2005) and DTMR (2011) still acknowledge that the infrastructure operating costs are part of the denominator of the BCR. It is likely that BCRs calculated with different formulas will be compared, thus creating more distortions in the evaluation process. Most BCA reports do not contain, which BCR formula has been applied, thus harmonisation of results becomes difficult. The benefit cost analysis of the Warrego Highway Investment Strategy is an example of a program of works containing several projects where maintenance cost reductions were estimated to be more than 40 per cent of the capital cost (TMR, 2010). If we assume the benefits of the project are twice the capital costs, the traditional BCR will be 39 per cent higher than the BCR_ATC⁵ for these projects. When maintenance costs increase after the construction of the project, the traditional BCR will be lower than BCR_ATC⁶, which increases the potential for distortions when projects with reduced maintenance costs are compared to projects with increased maintenance costs. Secondly, if the BCR_ATC formula is adopted, the purpose of the traditional BCR formula becomes redundant. The traditional BCR may not be the ideal measure to be applied to project prioritization but could still be a useful indicator to gauge overall returns to road agency expenditure.

4. Net Present Value

---

Net present value (NPV) is the discounted present value of a stream of benefits and costs over time (ATC 2006a). The NPV represents the net gain in welfare to society from the construction of a project. The NPV is not a useful tool to be applied to the prioritization of roads given the existence of capital constraints. The NPV is recommended by Austroads (Austroads 2005) and the Australian Transport Council (ATC 2006c) to be the most appropriate measure for selecting from mutually exclusive project options. The option with the highest NPV is considered the most viable option and is submitted for funding. The logic behind this assumption is that any increase in NPV is an increase in welfare over the next best alternative (invest in government bonds or marginal project with NPV of zero).

In an environment consisting of perfect information and complete efficient allocation of funds amongst all sectors in the economy, selecting the option with the highest NPV would maximize consumer welfare as the next best alternative has an NPV of zero. Unfortunately, these circumstances are rare; government sectors of the economy are either underfunded or overfunded (Arrow 1974). An underfunded sector operating efficiently will have some projects with NPVs above zero, which are not funded. An overfunded sector will have projects with NPVs below zero, which are funded. In the scenario of an underfunded sector, the option with the higher NPV may not be best option to select if the additional capital could have been allocated elsewhere at a higher return. Likewise, for an overfunded sector, an option with a higher NPV and lower capital cost may not be the most favourable option if the next best option has a negative return greater than the negative incremental return of the option with the higher capital costs.

Determining the project option with highest NPV while allocating funding based on the BCR can produce conflicting outcomes. Table 1 presents an example of a project with mutually exclusive options and two other unrelated projects, which are funded from the same pool of money ($120,000).

Table 1: Options Analysis Example (Scenario 1)

The outcome of the options analysis indicates that option 1A is the preferred mutually exclusive option (highest NPV) yet option 1A will be ranked below both projects 2 and 3 as these projects have higher BCRs. If option 1B was selected instead, project 1 would be ranked above projects 2 and 3. In the case presented in Table 1, choosing option 1B rather than option 1A will maximize welfare⁷ given the budget constraint, which only enables two projects to be constructed. The reason is not that selecting the option with the higher BCR is the efficient choice but the projects competing for funds have a BCR greater than 1A but lower than 1B.

If we replay the scenario given in Table 1 but reduce the BCRs of projects 2 and 3 to below 1.67, the outcome will be different. Table 2 contains this new scenario.

Table 2: Options Analysis Example (Scenario 2)

In this new scenario, if either project options are selected, project 1 will be ranked above projects 2 and 3 based on the BCR. Under these circumstances, the selection of option 1A will maximize welfare⁸ given the budget constraint.

From the two examples given above, we can see that selecting the option with the highest NPV sometimes leads to the selection of the optimal option but not always. Therefore selecting the mutually exclusive project option with the highest NPV may not result in the socially optimal outcome if the opportunity cost of capital is uncertain and not entirely reflected by the discount rate.

5. First Year Rate of Return

---

The first year rate of return (FYRR) as described in the ATC guidelines is a measure of the optimal start time of a project subject to a number of constraints. The constraints given by the BTRE (2005) are monotonically increasing benefits, the ability to change the start date of construction and an infinite asset life. The ATC guidelines prescribes that the optimal start time of a project should occur when the FYRR equals the discount rate. If the FYRR is greater than the discount rate, the project should have commenced at an earlier date. If the FYRR is less than the discount rate, the project should be delayed to the year when FYYR is greater or equal to the discount rate.

The first constraint of monotonically increasing benefits is rarely a factor as road user costs normally increase over time because of road deterioration and increasing traffic volume. Higher road user costs in the base case usually results in higher benefits. The second constraint of flexible construction start dates is not a factor as the optimal start date is irrelevant if the start date of construction is not flexible. The third constraint of infinite asset life posses the largest issue for the FYRR, as most road infrastructure projects do not have an infinite life. Typical road asset lives are given in Table 3.

Table 3: Life of Assets

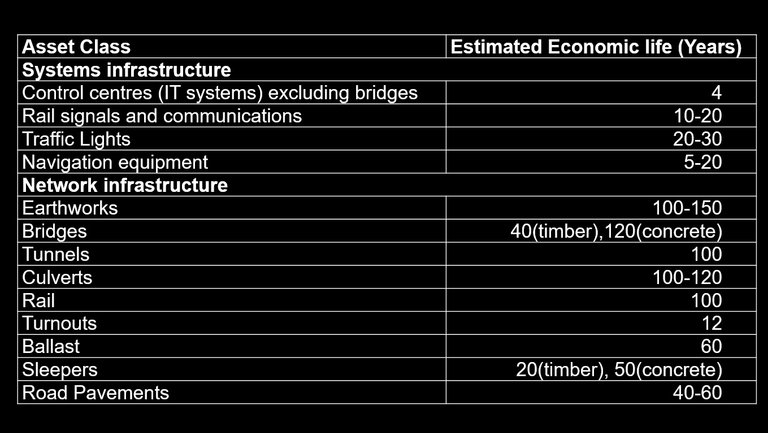
Source: Table 1.5.4, ATC 2006b

Most road project evaluations use an evaluation period of 30 years (Austroads 1996) and 10 to 15 years for intersection evaluations (DTMR 2011). The value of the asset for the remaining years is calculated as a residual value. The finite evaluation period of road projects undermines the strength of the FYRR as an indicator of the optimal start time for a project, as delaying a project creates the possibility of additional benefits from an additional year of life when a project is delayed. Comparing the FYRR to only the discount rate excludes the impact of this additional year. This additional year can be quite large even after discounting if the capacity of the road approaches saturation towards the end of the asset life of the road. Walters (1961) established an almost exponential increase in costs as roads approach saturation.

6. Proposed Solutions

---

The options analysis stage of project evaluation needs to be consistent with the prioritization stage amongst competing projects. Selecting a mutually exclusive option using either the NPV or the BCR when the BCR is applied to prioritizing of projects may not lead to an optimizing outcome. The first course of action should be to remove the BCR as the economic evaluation measure applied to project prioritization. Conflicting definitions of the BCR hinder the effectiveness of this measure. The net present value per dollar investment (NPVI) and the net benefit investment ratio (NBIR) are two possible alternatives to the BCR, neither of these ratios have conflicting definitions and both ratios evaluate the project based on returns to investment rather than a relationship between costs and benefits. The formula for NPVI is given in Equation 3, while the formula for is NBIR is given in Equation 4.

Equation 3: NPVI

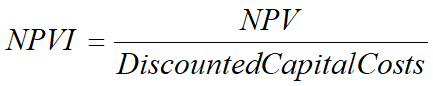
Equation 4: NBIR⁹

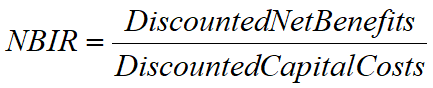
The NPVI is simply the NPV divided by investment costs, while NBIR is the equivalent to the ATC definition of the BCR minus the confusion with any other previous definitions. In this paper, the NBIR has been used as the economic measure applied to project prioritization, the NPVI would work as an equally effective measure to be applied to project prioritization.

If both options analysis¹⁰ and prioritization is conducted with the NBIR, the optimal projects may still not be selected. Therefore, we are presented with the quandary of how to marry the options analysis stage with the project prioritization stage. The NBIR of the marginal project¹¹ (NBIR_MP) could act as a key yardstick in the synchronisation process. Unfortunately, the NBIR_MP will only be revealed after the options analysis stage for the projects in the current financial year have been completed. A suitable compromise would be the use of the previous year’s NBIR_MP as the yardstick for the options analysis stage. The NBIR_MP is not likely to vary much from year to year, if the economic and social environment does change dramatically in one year. The trend in the NBIR_MP can be used to determine if road infrastructure is adequately funded.

In the options analysis stage, the NBIR_MP should be compared to the incremental net benefit investment ratio (INBIR). The INBIR is the additional net benefit from the increase in capital cost of a project option over another project option, the formula for INBIR is given in equation 5.

Equation 5: INBIR¹²

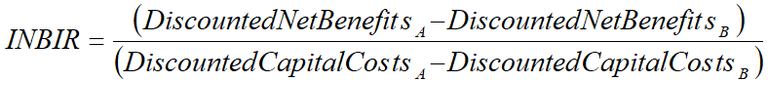
A = Project Option A
B = Project Option B

The additional benefits per dollar invested from the additional capital of the option with the larger capital expenditure should be greater than the NBIR_MP (opportunity cost of next best alternative) in order for the option with higher capital value to be considered optimal.

If we replay the first scenario given in Table 1 with the newly defined decision criterion, assuming current year NBIR_MP = previous year NBIR_MP and costs = capital, option 1B would be selected as shown in equation 6.

Equation 6: Compare BCR in scenario 1

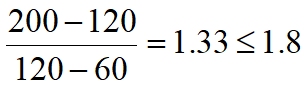
If we replay the second scenario given in Table 2, option 1A would be selected instead as shown in equation 7.

Equation 7: Compare BCR in scenario 2

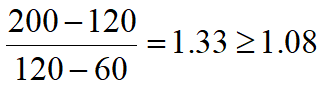
Comparing the INBIR with the NBIR_MP will result in the selection of the most economically viable option for as long as the NBIR_MP or the closest available proxy is representative of the marginal project for the current financial year. Comparing the INBIR with the NBIR_MP will also reduce the impact of an imperfect discount rate as INBIR and NBIR_MP will be subject to the same discrepancies¹³, thus negating some of issues relating to discount rates raised earlier in the paper.

The optimal timing of the start of construction of the project is not normally a high priority issue as the decision to commence the construction of a project is made once the project is deemed economically viable rather than based on the optimal timing of the project. Optimal timing measures can be used when competing projects with very similar NBIRs and the delay of a project maybe considerably more beneficial to one project compared to the other.

The ATC guidelines suggests the use of the NPV as a determinant of optimal timing as an alternative to the FYRR. The guidelines suggest that if a project is delayed and this delay causes the NPV to increase, the project should be delayed. Delaying a project and achieving a higher NPV indicates the welfare achieved from the project has increased. Increasing traffic volumes and deterioration of the road surface usually results in an increase of a project’s NPV over time if the same price year is applied in both evaluations. The use of the NPV as a determinant of optimal timing may result in the perpetual delay of most projects. A possible solution would be to compare the increases in NPV of projects with similar NBIRs and capital costs. The projects with the larger increase in NPV should be delayed to create the largest increase in welfare. This solution unfortunately, can be very time consuming and the re-evaluation of some projects is not always possible.

A possible alternative solution would be to use the internal rate of return¹⁴ (IRR). For marginal projects with similar NBIRs, the project with the higher IRR realises its benefits earlier (Osborne 2009), therefore, the project with the higher IRR benefits less from a delay than the project with a lower IRR. This statement can be proven mathematically by demonstrating the relationship between IRR and the increase in NPV resulting from a one-year delay in construction. The increase in NPV of a project because of a one-year delay in construction is given in Equation 8 and the formula for IRR is given in Equation 9¹⁵ .

Equation 8: Change in NPV¹⁶

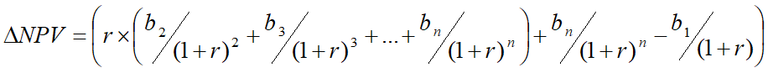
Equation 9: IRR

If in the nth year of the evaluation, benefits were to decrease by x and the first year of benefits were to increase by x/(1+r)n-1 such that the NPV is constant¹⁷, the increase in NPV from a delay of one-year would now equal to Equation 10.

Equation 10: Increase in NPV from one delay

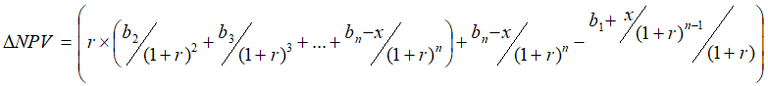
The decrease in the change in NPV is obtained by subtracting Equation 10 from Equation 8 and is given in Equation 11.

Equation 11: Equation 8 - Equation 10

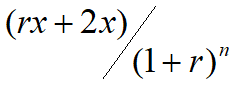
The formula for the IRR after the adjustment by x is given in Equation 12.

Equation 12: IRR with adjusted benefits

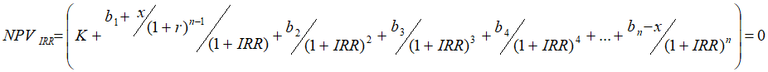
Equation 12 proves that the change in x will increase the IRR as x/((1+r)n-1(1+IRR)) > x/(1+IRR)n, when IRR>r, which occurs when NPV>0. To maintain an NPVIRR of zero, a higher IRR is required. Derivations of changes in NPV can be found in Appendix A. The proposed IRR criterion for project timing based on mathematical evidence is that projects with an IRR less than the IRR of the marginal project should be delayed.

A definitive mathematical relationship between changes in NPV resulting from a delay in construction and the IRR cannot be easily derived because of the nature of the formula of the IRR. The simplest methods of demonstrating the relationship is through examples and diagrams. The relationship between NPV, distribution of benefits and IRR is shown in Figure 1.

Figure 1: Benefit Distribution (prescribed discount rate vs. internal rate of return)¹⁸

Area A represents benefits discounted by the IRR, which is equivalent to the cost of the project. Area A and Area B combined represents benefits discounted by the prescribed discount rate. Area B is approximately equivalent to the NPV¹⁹ . Figure 1 diagrammatically represents the distortion IRR creates in favour of benefits obtained early in the life of the project. Any increase in benefits in the latter years of the project’s life will be more heavily penalised by a discount rate equal to the IRR, hence, further illustrating the indirect relationship between changes in NPV from a delay in construction and the IRR.

The application of IRR as a measure of the optimal start time of a project has a number of advantages over other measures. The IRR reflects benefits throughout the project life and not just the benefits in the first year; therefore, possible spikes in benefits or costs will cause minimal distortions to results²⁰ and, the benefits of the final year of the evaluation²¹ will be incorporated. Multiple calculations of the IRR are not required as the IRR has an inverse relationship to changes in NPV from delays in the construction of the project. The chances of perpetual delay of projects using the proposed IRR criterion are small as IRR and NPV have a direct relationship²² .

Table 4 contains an example of four projects; each project has a different distribution of benefits to test the response of different economic measures of the optimal start time of construction of a project.

Table 4: Optimal start time, year 0 or year 1

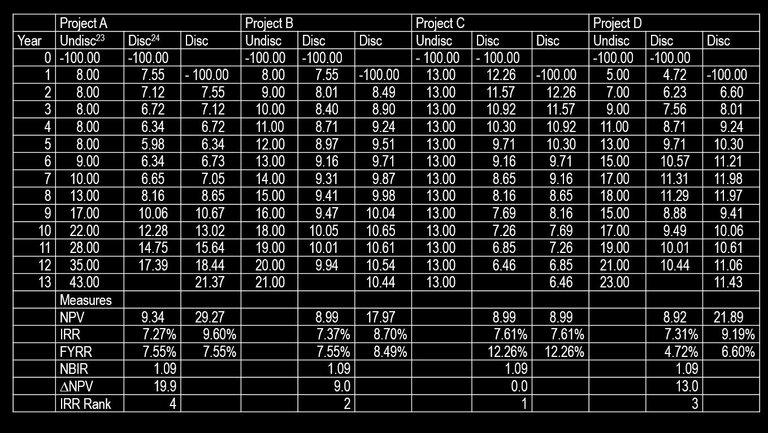
The FYRR implies only project D should be delayed²⁵ . If delaying the project depends upon increasing the NPV, projects A, B and D should be delayed. According to the proposed IRR criterion, Project A should be considered the most likely project to be delayed and Project C, the least likely. The highest ranked projects according to the IRR are the projects with the smallest increase in NPV from a delay of one year. If we assume that benefits do not fluctuate wildly from year to year and NPV>0, the IRR should be lower for marginal projects that will benefit the most from delayed construction.

The application of the IRR as a measure of the optimal start time of a project is subject to a number of limitations. The variation in IRR should only be used when projects have very similar NBIRs and are considered as marginal projects. When projects have an NPV<0, the decision criterion should be reversed as the IRR is below the prescribed discount rate, thus favouring projects, which generate benefits later in their life. The practitioner evaluating the project will not be able to make a recommendation regarding the timing of the project, as information regarding other marginal projects is unlikely to be available. The comparison of IRR will need to be made by the decision makers who prioritizing the projects. This process should be simple as long as the number of marginal projects is small.

There is not an easy solution to the optimal timing issue but considering this issue may only be relevant when considering marginal projects, the choice of this criterion is not as crucial as the choice of criterion applied to prioritization. The IRR is probably the most useful guide to determining which project should be delayed and which project should be constructed in the current financial year. Re-calculating the NPV of marginal projects could provide an accurate measure of the increase the projects may have in welfare but a single measure is a simpler option. If doubts arise about the implication of the IRR, recalculating the NPV is still a viable option to determine the optimal timing of the project. The IRR can serve other purposes, which renders it a useful inclusion in an analysis. One of these other purposes is discussed in Section 7.

7. Application of results at the program level

---

The results of an evaluation need not be limited in application to the current projects but can be applied to the program of works as a whole. The ultimate goal of any program is to maximize net social welfare from the allocated funds to road infrastructure. This goal can be achieved by collating the appropriate information from the individual projects.

The IRR of the marginal project (IRR_MP) can be used as a discount rate for projects in the next financial year²⁶ . The use of the IRR_MP as a discount rate could help simplify the planning process if NBIR_MPs are different from zero. An NBIR calculated using IRR_MP as a discount rate invokes the simple selection criterion of NBIR>1. The IRR_MP can also be used as a determinant for the standard discount rate applied to all projects within the state. The wide range of proposed discount rates discussed earlier in this paper provides evidence of the lack of information about the opportunity costs of individual projects. IRR_MP could prove to be a useful measure to refine the discount rate given that the marginal project could provide a more useful benchmark of the opportunity cost of proposed projects.

The net present value (NPV) has not been included in the project decision criteria simply because of issues such as imperfect information; lack of mobility of funding for road infrastructure and capital constraints and unreliable discount rates. The objective of the Government should be to maximize the NPV of infrastructure as a whole rather than for individual projects. The program of works with the highest NPV, assuming limitations in the transferability of capital, is the program of works, which optimizes measurable welfare.

The NBIR_MP can also serve a purpose at the program level. The NBIR_MP when perfect resource allocation exists is one. Any value other than one is an indication of inefficient resource allocation. A NBIR trend for the incremental project can be used to establish if resource allocation is improving. In Figure 2, four possible trends of NBIR for the marginal project are considered.

Figure 2: Trends in NBIRMP

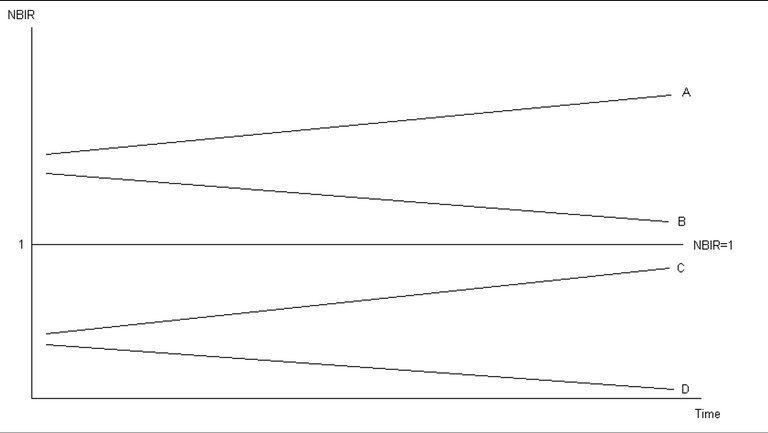
If trend A is observed, road infrastructure is underfunded and resource allocation is becoming less efficient. If trend B is observed, road infrastructure is underfunded but resource allocation is improving. If trend C is observed, road infrastructure is overfunded and resource allocation is improving. If trend D is observed, road infrastructure is overfunded and resource allocation is becoming less efficient. These trends should only be used as an indicator of efficiency if fund allocation is likely to be inflexible.

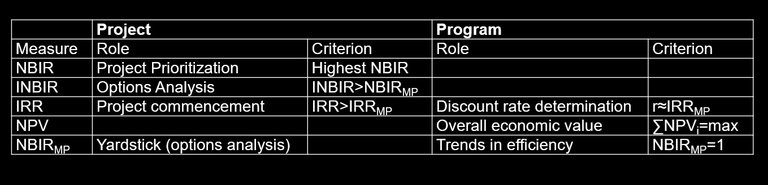
8. Summary of proposed economic measures and decision criteria

---

The economic measures proposed in this paper to evaluate road project infrastructure are not radically different from those proposed by the ATC (BCR, NPV and FYRR) but the outcome of their effective application will improve the quantitative assessment of projects and may result in a vastly different ranking of projects²⁷ . The economic measures, which can be applied at the program level, provide decision makers with instruments to improve the accuracy of resource allocation over time. The proposed economic measures and decision criteria are summarized in Table 5.

Table 5: Summary of Proposed Economic Measures and Decision Criteria

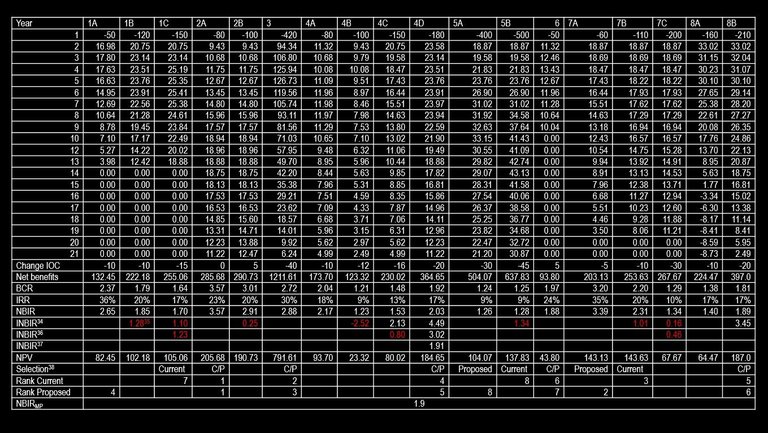
To demonstrate the application of these economic measures and decision criteria, a group of hypothetical projects have been compared using the proposed criteria and the current criteria. In this hypothetical example, assume that an estimated $1,000,000 are allocated to road infrastructure, the discount rate is 6 per cent and the previous year’s NBIR_MP is 1.9. Results and quantitative ranking of the projects are given in Table 6.

Table 6: Results and Ranking of Hypothetical Projects (NPV and Capital in $’000)

Ranking the options using the NPV rather than the INBIR has resulted in a number of different selections at the options analysis stage, which has resulted in a different order of project prioritization. Under the current method, option 1C is selected in the option analysis stage but is not funded. Under the proposed method, option 1A is selected in the options analysis and is funded. Project option 7A is funded in the proposed method and project option 7B is funded under the current method. The discounted benefits, costs and detailed results are given in Appendix B.

Prioritizing projects based on BCR rather than NBIR can also change the order projects are ranked. Project 6 is ranked ahead of project 8B using the BCR as Project 6 reduces infrastructure operating costs (IOC) while project 8B increases IOC. Applying the NBIR to prioritization of projects, results in the prioritizing of Project 8B ahead of Project 6, this has in turn resulted in Project 6 not receiving funding in the current financial period. The proposed changes to project ranking has resulted in an improved total NPV and a more efficient outcome to society.

9. Conclusion

---

The ATC economic measures and decision criteria generally serve the purpose of determining the economic viability of individual projects but do not provide decision makers with the most useful quantitative assessment of projects to be considered for prioritization. Different projects are likely to be subject to different criteria depending on the interpretation of the definitions of the BCR applied to evaluate them. The inconsistency of the methodology of evaluating mutually exclusive options and the methodology applied to prioritizing projects sometimes results in the selection of less optimal project options. This paper proposes the application of new economic measures with new decision criteria based on mathematical evidence and examples of when the proposed measures achieve a more efficient allocation of funds amongst competing projects. The results obtained from the proposed economic measures for individual projects can also be applied to program analysis and the long run allocation of resources.

To add more rigour to the analysis of the economic measures and decision criteria discussed in this paper, a detailed analysis of actual project evaluations should be conducted. This analysis could be used to determine how frequently the issues mentioned in this paper occur and the extent the proposed solutions remedy these issues. Documented evidence of wrongly prioritized projects based on the ATC economic measures and decision criteria would probably be necessary to formalize any significant changes to the current standards.

Appendix A: Mathematical Derivation of Change in NPV

∆NPV³³ is derived as follows:

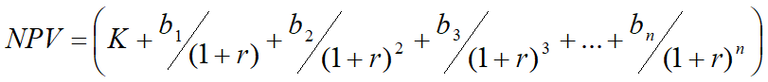
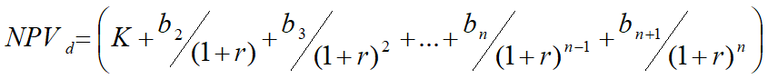
∆NPV = NPV_d - NPV

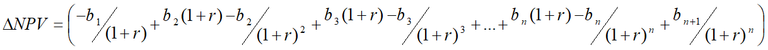
Assume bn+1 = bn and simplify:

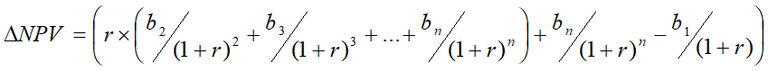
∆NPV is derived as follows when x is included:

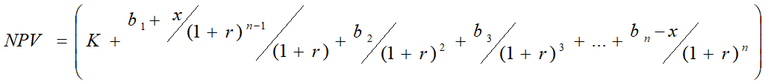
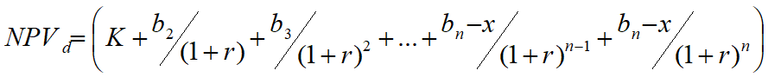
∆NPV = NPV_d - NPV

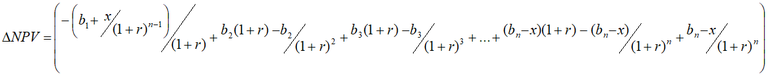
Simplify:

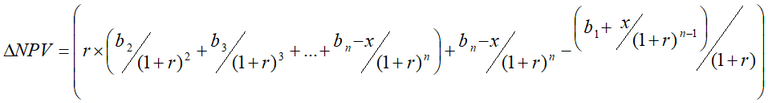
Appendix B: Discounted Benefits and Costs and Results of Hypothetical Projects (Benefits and Costs in $‘000)

End Notes

1. Unabridged version of ‘Proposed Modifications to the Cost Benefit Analysis Decision Criteria for Road Project Evaluation to Improve Decision Making’ published in AST&L Transport Journal.
2. Prescribed discount rate
3. Gamma discounting is a process of discounting benefits/costs at different rates depending on the period these benefits/costs occur; Weitzman takes the stance that benefits/cost in the distant future should have a smaller discount rate applied to them than benefits/costs in the near future.
4. Infrastructure Operating Costs includes maintenance and rehabilitation costs
5. BCR=2/(1-0.4)=3.33, BCR_ATC =2+0.4=2.4, (BCR/ BCR_ATC)-1=38.75%
6. According to Bray, D. J., and Tisoto, P. 2007, the BCR is lower than the BCR_ATC when the BCR is above 1 and higher than the BCR_ATC when the BCR is below 1; this statement holds true as long as maintenance costs are higher in the project case.
7. If option 1A is selected, overall NPV=50,000+48,000=98,000 (project 2 + project 3), if option 1B is selected, overall NPV=60,000+50,000+110,000 (project 1 + project 2). Maximizing the NPV (gain in welfare) of the whole program of works should be the priority of the department (Campbell and Brown 2003), usefulness of NPV at the program level is discussed later in the paper.
8. If option 1A is selected, overall NPV=80,000 (project 1), if option 1B is selected, overall NPV=60,000+10,000=70,000 (project 1 + project 2)
9. The formula for NBIR = formula for BCR_ATC as discounted net benefits are assumed to equal discounted benefits minus infrastructure operating costs
10. From this point onwards, mutually exclusive options and options will be referred to, as just options as the proposed treatment of mutually exclusive and non-mutually exclusive options are the same.
11. The marginal project or incremental project is the project with the lowest economic value per dollar invested, which has been ranked according to monetised economic benefits. The NBIR of the marginal project can act as a NBIR cut-off value for which other projects can be compared too. Projects with lower economic value per dollar and are not prioritized based on monetised economic benefits should not be considered.
12. The capital costs of project option B should be larger than the capital costs of project option A
13. We are assuming INBIR and NBIR_MP are subject to the same discount rate.
14. The IRR is the value of the discount rate when the NPV is zero. The IRR can only be applied to projects, which have at least one year of negative returns and at least one year of positive returns.
15. For simplicity, the capital costs have been assumed to occur only in the first of the evaluation.
16. For simplicity, the benefits in year n are assumed to equal benefits in year n+1
17. x is assumed to be positive.
18. The relationship in distribution of benefits in Figure 1 can be derived using the formula: (1+r)n/(1+IRR)n , where (1+r) n/(1+IRR) n decreases as n increases when IRR>r.
19. This statement is made based on the assumption that all capital is invested in the project in year 1.
20. Benefits could fluctuate in years when road closures occur, rehabilitation in the base case improves the quality of the road surface or when traffic diverts because of road closures.
21. The final year of the evaluation (year n) makes an appropriate proxy for year n+1.
22. If IRR_MP remains approximately constant over time and the IRR of the project increases each year, IRR will eventually be greater than IRR_MP.
23. Undiscounted costs and benefits expressed in dollars
24. Discounted costs and benefits expressed in dollars at a discount rate of 6%
25. The criterion of FYRR>discount rate has been applied to assess optimal timing of projects
26. This is an application of social opportunity cost discussed in Section 2
27. See Table 6 for possible differences in the ranking of projects using the proposed measures and criteria.
28. Projects are represented by numbers and options are represented by letters
29. The traditional definition of the BCR is used in Table 6 (infrastructure operating costs are in the denominator of the formula).
30. Ranking of projects is according to BCR and options according to NPV
31. Ranking of projects is according to NBIR and options according to INBIR located in Appendix B
32. Capital has been allowed to exceed the budget by $50,000. If the budget of $1,000,000 were not allowed to be exceeded, project 6 would be considered for the next financial year rather than project 8B as project 8B has the highest NPV without exceeding the budget.
33. NPV_d is the NPV after the construction of the project has been delayed by a year.
34. The INBIR is between options A and B in B column; B and C in C column; and C and D in D column.
35. INBIR values in red do not meet the criterion of INBIR>NBIRMP.
36. The INBIR is between options A and C in C column, and B and D in D column.
37. The INBIR is between options A and D in D column.
38. Current selection is based on current criterion (NPV), proposed selection is based on proposed criterion INBIR>NBIR_MP and C/P occurs when both criteria obtain the same option.

References

Arrow, K, J. (1974): Limited Knowledge and Economic Analysis, The American Economic Review, 64, (1), 1-10

Australian Government (2008): Outline of Infrastructure Australia’s Prioritization Methodology, Australian Government, Infrastructure Australia

Australian Transport Council (2006a): National Guidelines for Transport Systems Management in Australia, 3 Appraisal of initiatives, Commonwealth of Australia, Canberra

Australian Transport Council (2006b): National Guidelines for Transport Systems Management in Australia, 4 Urban transport, Commonwealth of Australia, Canberra

Australian Transport Council (2006c): National Guidelines for Transport Systems Management in Australia, 5 Background material, Commonwealth of Australia, Canberra

Austroads (1996): Benefit Cost Analysis Manual, Austroads, Sydney

Austroads (2005): Guide to Project Evaluation, Part 2: Project Evaluation Methodology, Austroads, Sydney

Baumol, W. J. (1968), On the Social Rate of Discount, The American Economic Review, 58, (4), 788-802

Baumol, W. J. (1969): On the discount rate for public projects, The analysis and evaluation of public expenditures: The PPB System, Joint Economic Committee Print, U.S. Government Printing Office, Washington, D.C. 1, 489-503

Booz Allen Hamilton (2007): Draft Cost Benefit Analysis Guidelines for CASA, Canberra (Unpublished)

Bray, D. J. and P. Tisato (2007): An Examination of Some Issues Related to Benefit Measurement and the Benefit Cost Ratio, 30th Australasian Transport Research Forum, Melbourne

Bureau of Transport and Regional Economics, (2005): Report 110: Risk in cost-benefit analysis, Department of Transport and Regional Services

Campbell, H. F. and R. P. C. Brown (2003): Benefit-Cost Analysis Financial and Economic Appraisal Using Spreadsheets, Cambridge University Press, Cambridge

CC Pace, 2003, Prioritizing Projects to Maximize Return on Investment, accessed 26th March 2010, available at www.ccpace.com

Department of Transport and Main Roads, (2011): Cost benefit analysis manual, Brisbane

Department of Transport and Main Roads, (2010): Rapid Benefit Cost Analysis – Warrego Highway Investment Strategy

Osborne, M. J., (2009): A resolution to the NPV – IRR debate? The Quarterly Review of Economics and Finance, Middlesex University Business School, London

Perkins, F., (1994): Practical Cost Benefits Analysis, Macmillan, South Melbourne

Roads and Traffic Authority, (2006): Economic Analysis Manual, Version 2, Sydney

Ross, S. A. (1995): Uses, Abuses, and Alternative to Net-Present-Value Rule, Financial Management, 24, (3), 96-102

Walters, A. A., (1961): the Theory and Measurement of Private and Social Cost of Highway Congestion, Econometrica, 29, (4), 676-699

Weitzman, M. L. (1998): Why the Far-Distant Future Should Be Discounted at Its Lowest Possible Rate, Journal of Environmental Economics and Management, 36, 201-201

Weitzman, M. L. (2001): Gamma Discounting, The American Economic Review, 91, (1), 260-271