The logistic map in R
I am just trying to learn the logistic map, so here are some notes and the R code snippets.
Basically what the logistic map does, is a equation that returns the next value based on current value.
The formula is Xn+1 = R * Xn * (1-Xn).
- Xn is the value of X in the nth iteration.
- Xn+1 is the next value of Xn, which we calculate.
- R is the parameter.
This equation has been used in several real life problems to model the situation. One example is population growth.
In its crude form, it looks like this when coding in R.
R=3
x0=0.5
x1=R*x0*(1-x0)
x2=R*x1*(1-x1)
x3=R*x2*(1-x2)
x4=R*x2*(1-x3)
x5=R*x2*(1-x4)
x6=R*x2*(1-x5)
We can try to plot it and iterate over many rounds through a loop.
R=3
a=0.5
points<-c(a)
for (i in 1:30){
b<-R*a*(1-a)
a=b
points[i]<-a
}
plot(points)
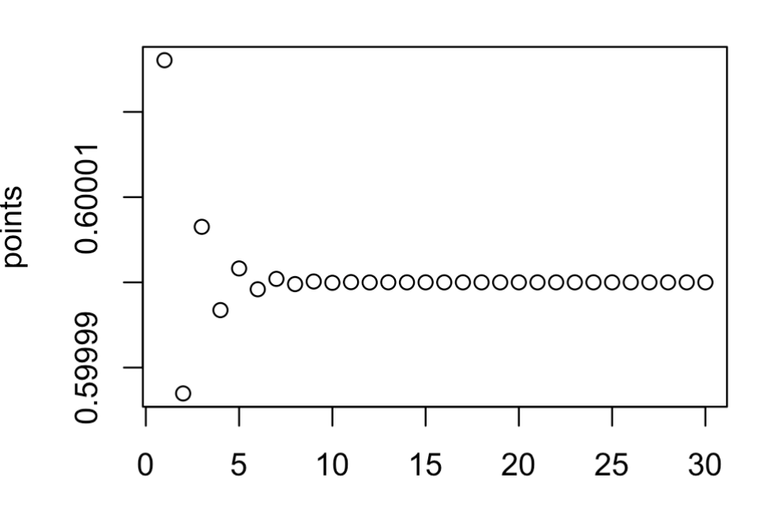
We see a stabilisation with R being 3. This is also call a fixed point when there is a stabilisation to a value.
Let's try with R being 3.4.
R=3.4
a=0.5
points<-c(a)
for (i in 1:30){
b<-R*a*(1-a)
a=b
points[i]<-a
}
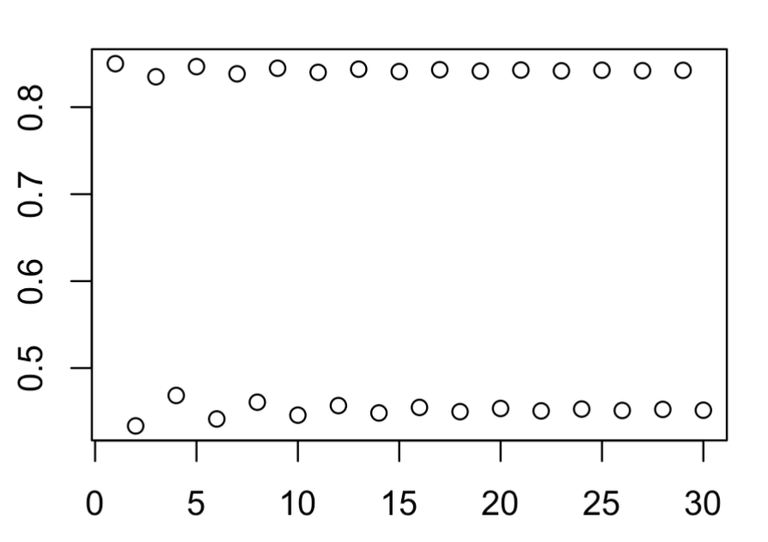
plot(points)
Now we see a bistable state, i.e. X value fluctuating up and down.
Apparently, at R of approximately 3.5699456, not far from 3.4, something strange starts to happen.
R=3.5699456
a=0.5
points<-c(a)
for (i in 1:30){
b<-R*a*(1-a)
a=b
points[i]<-a
}
plot(points)
The bistable states starts to be changed.
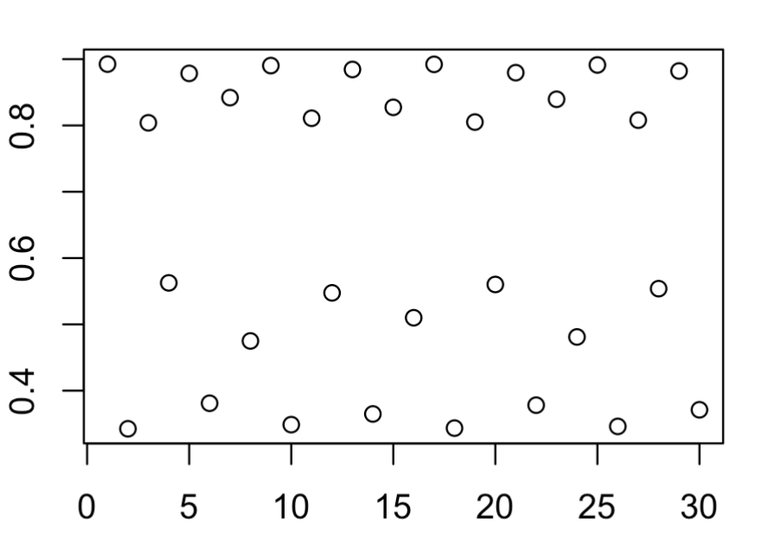
And when R is 3.65, some kind of messy plot emerges.
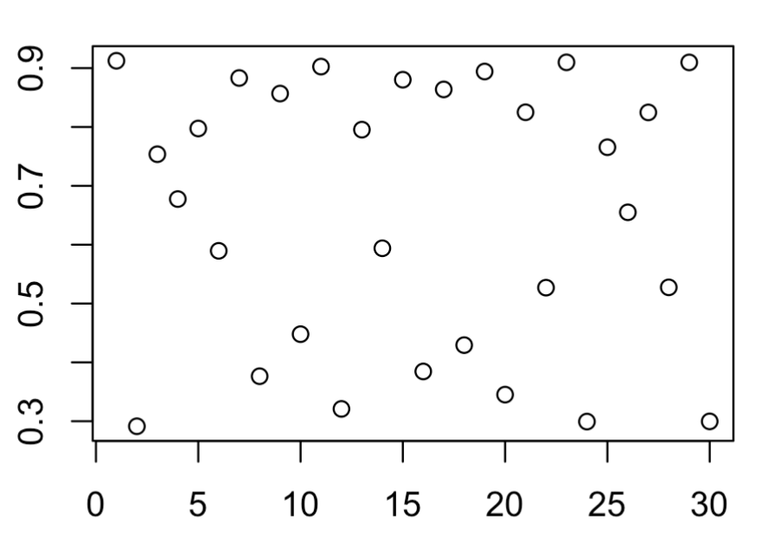
At R at 3.999999999999...
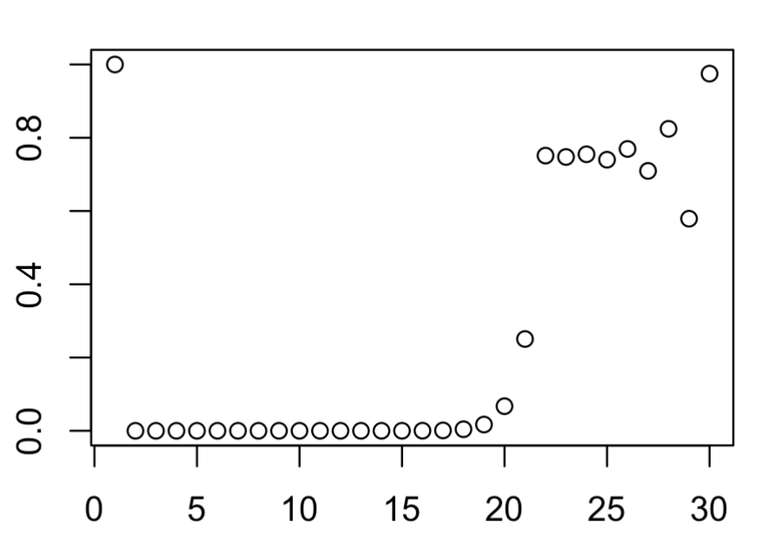
Finally, at R = 4.0. We get back another fixed point.
Congratulations @snippets! You have completed the following achievement on the Hive blockchain And have been rewarded with New badge(s)
Your next target is to reach 30 posts.
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPCheck out our last posts:
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.