▶️Watch on 3Speak - Odysee - BitChute - Rumble - YouTube - PDF notes

In this video I go over the end of chapter review questions covering the Vectors and the Geometry of Space chapter. There are 19 questions in total and serve as a good review on vectors, dot products, cross products, as well as the equations of lines, planes, and their applications. I also cover a few details, notably the distance between a point and a line, differently than I had in my earlier videos covering the chapter; so make sure to watch this video!

Timestamps

The topics covered as well as their timestamps are listed below.

• Intro: 0:00
• Calculus Book Reference: 0:58
• Sections in Calculus Book Chapter: 1:14
• Topics to Cover: 1:57
• Review: Concept Check: 19 Questions: 2:19

1. Question 1: Vector vs scalar: 2:54
2. Question 2: Vector addition: 3:33
3. Question 3: Multiplying vector by a scalar: 6:14
4. Question 4: Position vector: 7:45
5. Question 5: Dot product: 9:20
6. Question 6: Applications of dot product: 11:20
7. Question 7: Scalar and vector projections: 19:05
8. Question 8: Cross product: 21:02
9. Question 9: Applications of cross product: 27:33
10. Question 10: Parallelogram and Parallelepiped: 32:44
11. Question 11: Vector perpendicular to plane: 34:28
12. Question 12: Angle between 2 planes: 35:48
13. Question 13: Vector, parametric, and symmetric equations for a line: 37:04
14. Question 14: Vector and scalar equation for a plane: 40:46
15. Question 15: Parallel or perpendicular vectors and planes: 42:41
16. Question 16: Points on a line or plane: 46:22
    • Solution to (a): 3 Points on a Line: 46:40
    • Solution to (b): 4 Points on a Plane: 49:56
17. Question 17: Distances between Points, Lines, Planes: 52:08
    • Solution to (a): Distance from a Point to a Line: 52:30
    • Solution to (b): Distance from a Point to a Plane: 58:21
    • Solution to (c): Distance between Two Lines: 1:00:00
18. Question 18: Traces of a surface: 1:14:50
19. Question 19: Six types of quadric surfaces: 1:21:58

• Outro: 1:26:53

---

Playlists

Video sections - Vectors and the Geometry of Space

---

View Video Notes Below!

---

Become a MES Super Fan - Donate - Subscribe via email - MES merchandise

• MES Links webpage - MES Links Telegram - MES Truth

Reuse of my videos:

• Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.

Fight back against censorship:

• Bookmark sites/channels/accounts and check periodically.
• Remember to always archive website pages in case they get deleted/changed.

Recommended Books: "Where Did the Towers Go?" by Dr. Judy Wood

Join my forums: Hive community - Reddit - Discord

Follow along my epic video series: MES Science - MES Experiments - Anti-Gravity (MES Duality) - Free Energy - PG

---

NOTE 1: If you don't have time to watch this whole video:

• Skip to the end for Summary and Conclusions (if available)
• Play this video at a faster speed.
  -- TOP SECRET LIFE HACK: Your brain gets used to faster speed!
  -- MES tutorial
• Download and read video notes.
• Read notes on the Hive blockchain $HIVE
• Watch the video in parts.
  -- Timestamps of all parts are in the description.

Browser extension recommendations: Increase video speed - Increase video audio - Text to speech (Android app) – Archive webpages

---

Vectors and the Geometry of Space: Review

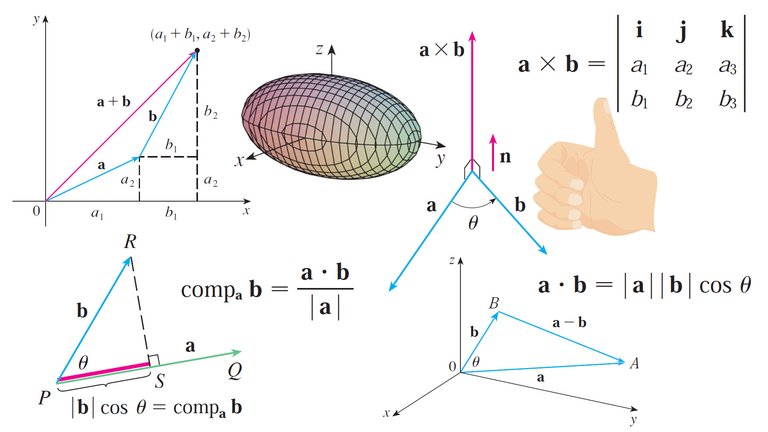
Concept Check: Review

---

Sections in Calculus Book Chapter

I have made a list of the sections in this particular chapter with links to the Hive post of the videos I have already finished.

Note that I have started splitting each long video into sections and made a playlist for each.

Vectors and the Geometry of Space

1. 3-D Coordinate Systems
2. Vectors
   • Complex Numbers as Rotation Matrices (Playlist)
3. The Dot Product - Playlist
4. The Cross Product - Playlist
   • Discovery Project: The Geometry of a Tetrahedron - Playlist
5. Equations of Lines and Planes - Playlist
   • Laboratory Project: Putting 3D in Perspective - Playlist
6. Cylinders and Quadric Surfaces - playlist
7. Review - playlist - Current Video
   • True-False Quiz
8. Problems Plus
   Vectors and the Geometry of Space

---

Topics to Cover

Note that the timestamps will be included in the video description for each topic listed below.

• Review: Concept Check: 19 Questions

1. Question 1
2. Question 2
3. Question 3
4. Question 4
5. Question 5
6. Question 6
7. Question 7
8. Question 8
9. Question 9
10. Question 10
11. Question 11
12. Question 12
13. Question 13
14. Question 14
15. Question 15
16. Question 16
    • Solution to (a): 3 Points on a Line
    • Solution to B: 4 Points on a Plane
17. Question 17: Distances between Points, Lines, Planes
    • Solution to (a): Distance from a Point to a Line
    • Solution to (b): Distance from a Point to a Plane
    • Solution to (c): Distance between Two Lines
18. Question 18
19. Question 19

Review: Concept Check

1. What is the difference between a vector and a scalar?
2. How do you add two vectors geometrically?
   • How do you add them algebraically?
3. If a is a vector and c is a scalar, how is ca related to a geometrically?
   • How do you find ca algebraically?
4. How do you find the vector from one point to another?
5. How do you find the dot product a ∙ b of two vectors if you know their lengths and the angle between them?
   • What if you know their components?
6. How are dot products useful?
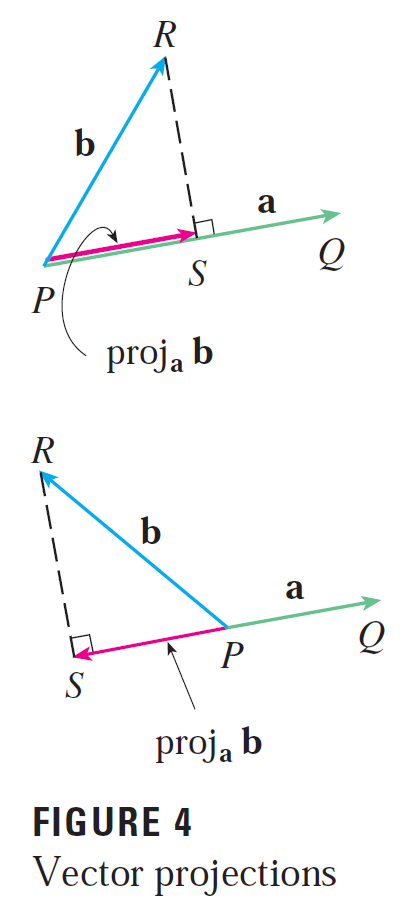
7. Write expressions for the scalar and vector projections of b onto a.
   • Illustrate with diagrams.
8. How do you find the cross product a × b of two vectors if you know their lengths and the angle between them?
   • What if you know their components?
9. How are cross products useful?
10. (a) How do you find the area of the parallelogram determined by a and b?
    (b) How do you find the volume of the parallelepiped determined by a, b, and c?
11. How do you find a vector perpendicular to a plane?
12. How do you find the angle between two intersecting planes?
13. Write a vector equation, parametric equations, and symmetric equations for a line.
14. Write a vector equation and a scalar equation for a plane.
15. (a) How do you tell if two vectors are parallel?
    (b) How do you tell if two vectors a perpendicular?
    (c) How do you tell if two planes are parallel?
16. (a) Describe a method for determining whether three points P, Q, and R lie on the same line.
    (b) Describe a method for determining whether four points P, Q, R, and S lie in the same plane.
17. (a) How do you find the distance from a point to a line?
    (b) How do you find the distance from a point to a plane?
    (c) How do you find the distance between two lines?
18. What are the traces of a surface?
    • How do you find them?
19. Write equations in standard form of the six types of quadric surfaces.

---

Question 1

What is the difference between a vector and a scalar?

Solution:

A vector is a quantity that has both a magnitude and direction, for example velocity.

A scaler is a quantity that only has a magnitude, for example temperature.

---

Question 2

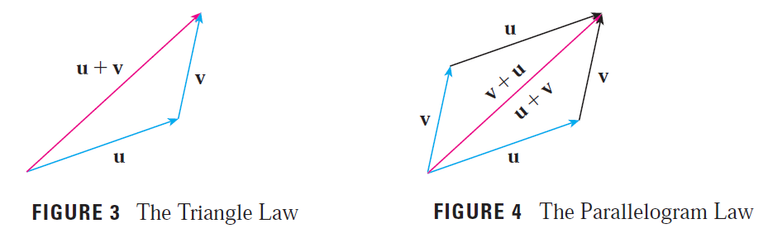
How do you add two vectors geometrically?

How do you add them algebraically?

Solution:

We can add two vectors geometrically using the Triangle or Parallelogram Law:

We can add two vectors algebraically by adding their components:

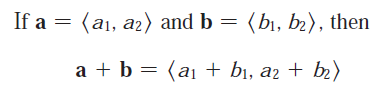
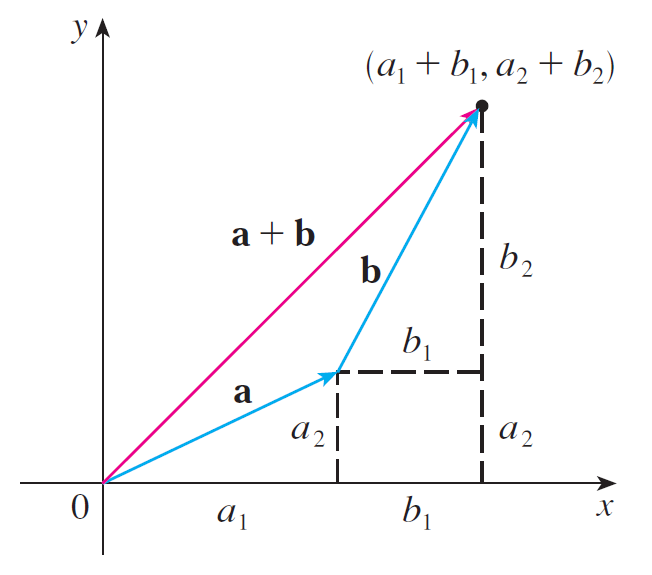
We can visualize the geometric and algebraic vector additions at the same time:

---

Question 3

If a is a vector and c is a scalar, how is ca related to a geometrically?

How do you find ca algebraically?

Solution:

Geometrically, ca shortens or extends a.

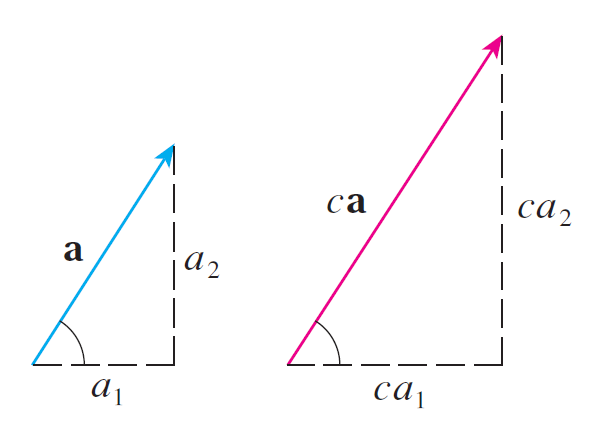
We can find ca by multiplying the components of the vector a by scalar c.

---

Question 4

How do you find the vector from one point to another?

Solution:

We can subtract the components of the initial point to the terminal point.

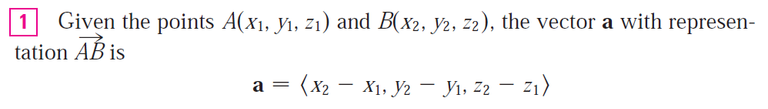
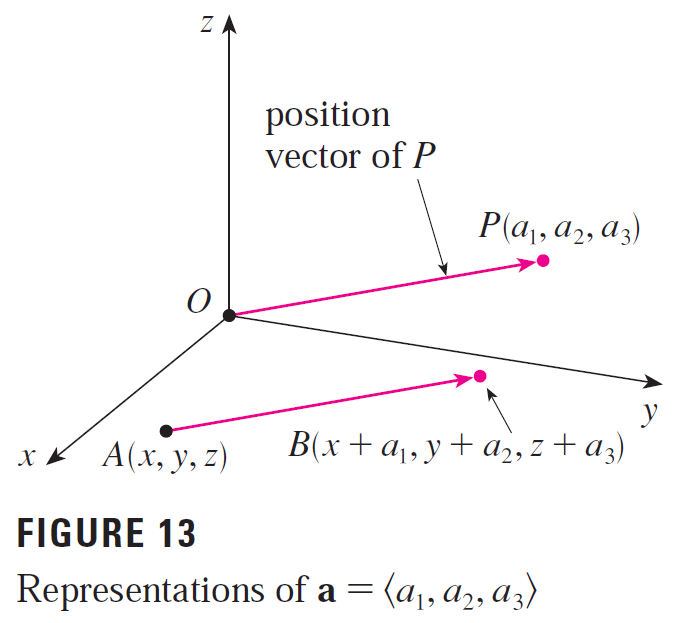
Question 5

How do you find the dot product a ∙ b of two vectors if you know their lengths and the angle between them?

What if you know their components?

Solution:

If we know the length of the vectors a and b as well as the angle between them, then we can find the dot product a ∙ b by the following formula:

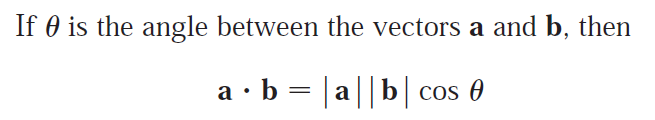
If we know the components of a and b then the dot product a ∙ b is given by the definition, which is the multiplication of corresponding components and adding them all together:

---

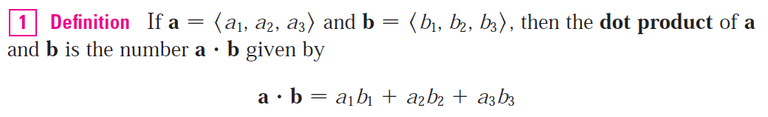
Question 6

How are dot products useful?

Solution:

Dot products have many useful properties.

(1) Determining the angle between 2 vectors.

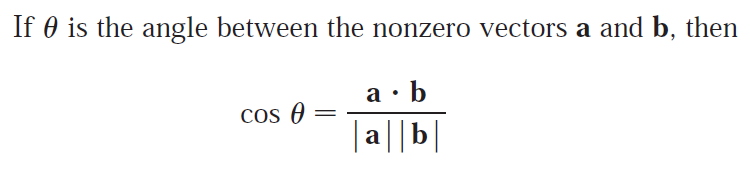
(2) Checks orthogonality: 2 vectors are orthogonal (perpendicular) if their dot product is zero (aka cos(90°) = 0).

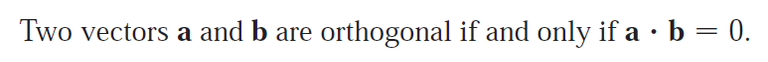
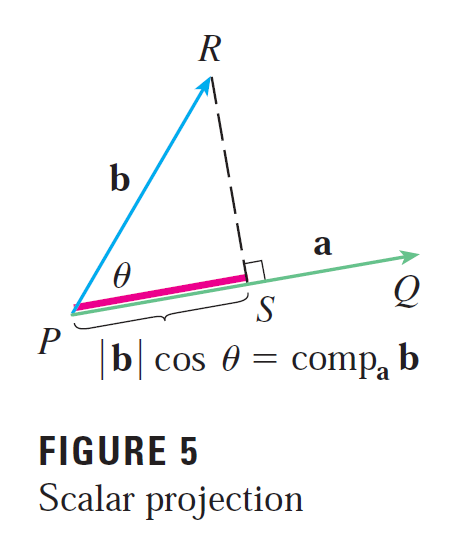
(3) Projecting one vector onto another.

(4) Calculating work done by a constant force.

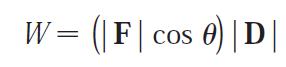
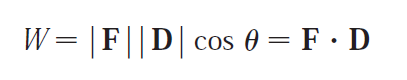
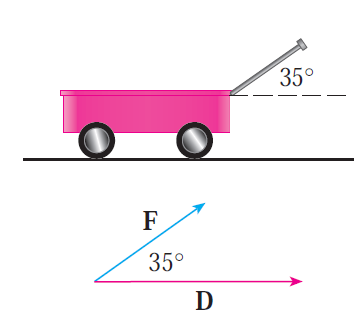
These properties are very useful in many applications such as physics, machine learning (dot product is fundamental in neural networks in measuring similarity between vectors), computer graphics, and engineering.

This was taken from ChatGPT: https://chatgpt.com/share/6e3be6a9-38d1-4ae7-852a-62977b6a492f

---

Question 7

Write expressions for the scalar and vector projections of b onto a.

Illustrate with diagrams.

---

Solution:

The scalar and vector projections of b onto a are shown below:

The projections are seen visually below:

---

Question 8

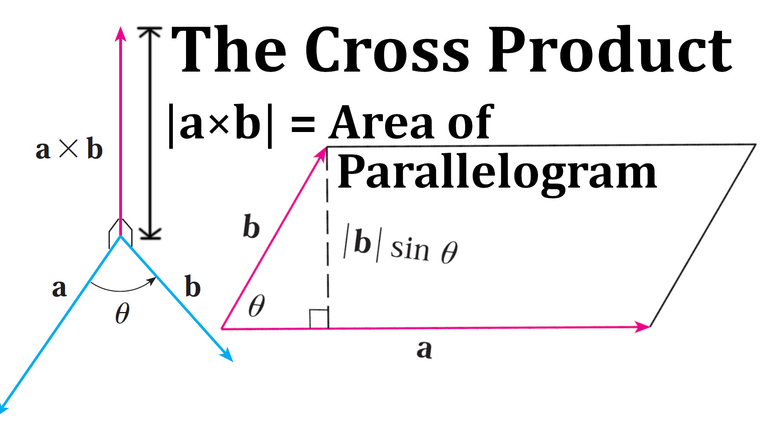
How do you find the cross product a × b of two vectors if you know their lengths and the angle between them?

What if you know their components?

Solution:

If we know the angle and lengths of two vectors, we can determine the length of the cross product via the following equation:

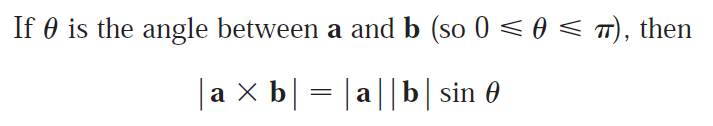
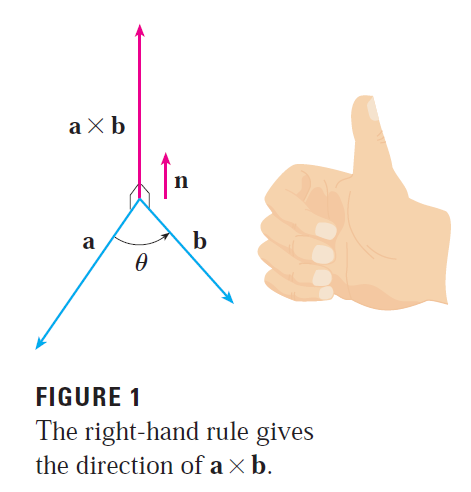
Note the right-hand rule gives the direction of the cross product and angle.

If we know the components of two vectors, we can compute the cross product via its definition:

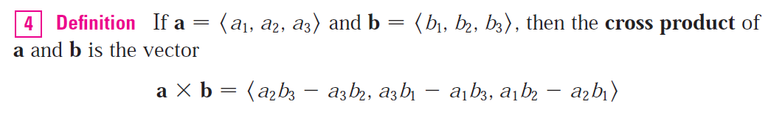
We can also use determinates and standard basis vectors to solve the cross product:

---

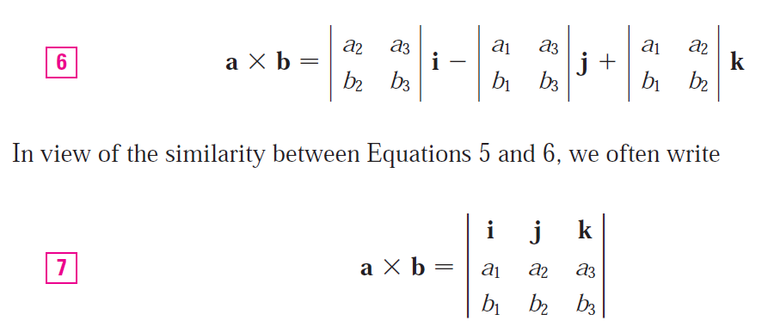
Question 9

How are cross products useful?

Solution:

Some useful properties of the cross product are listed below:

(1) Determining the Perpendicular Vector: The cross product is perpendicular to both of its vectors, thus allowing to find the normal vector of surfaces and planes.

(2) Calculating the area of a parallelogram.

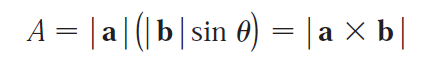
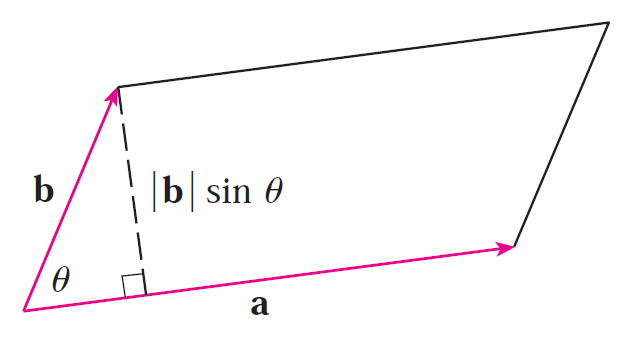
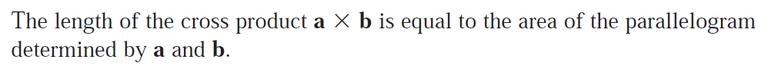
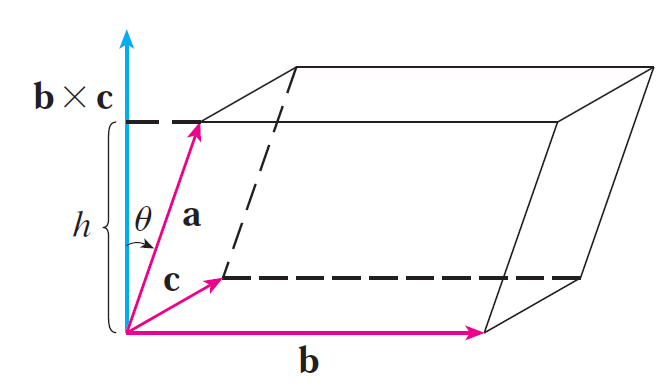
(3) Calculating the volume of a parallelepiped.

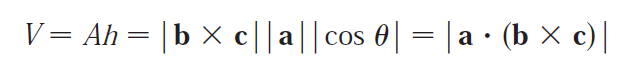
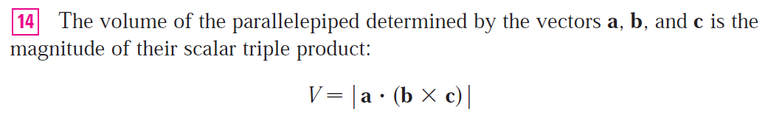
(4) Calculating Torque.

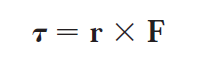
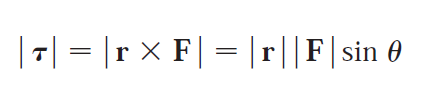
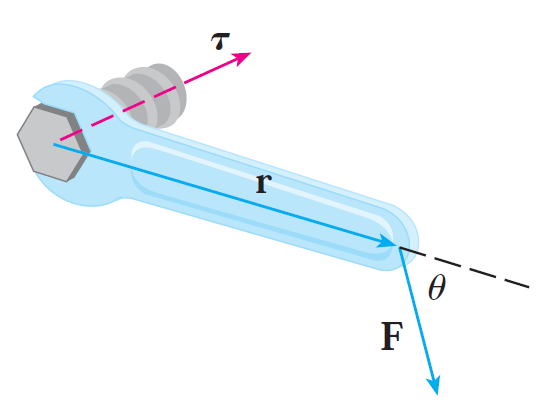
There are many more applications in physics, geometry, and computer graphics.

---

Question 10

(a) How do you find the area of the parallelogram determined by a and b?

(b) How do you find the volume of the parallelepiped determined by a, b, and c?

Solution to (a)

The area of a parallelogram is the length of the cross product of its two vectors.

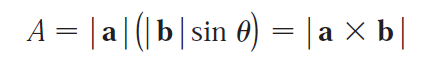
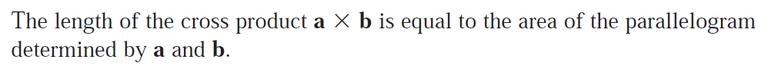
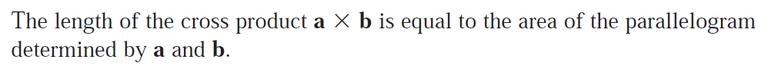
Solution to (b):

The volume of a parallelepiped is determined by the magnitude of the scalar triple product.

---

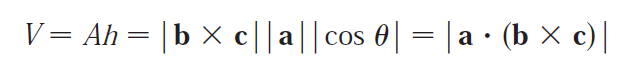
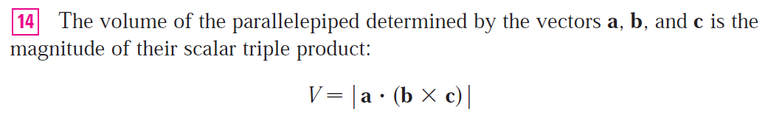
Question 11

How do you find a vector perpendicular to a plane?

Solution:

We can find a vector perpendicular to a plane by taking the cross product of any two non-parallel vectors on the plane.

---

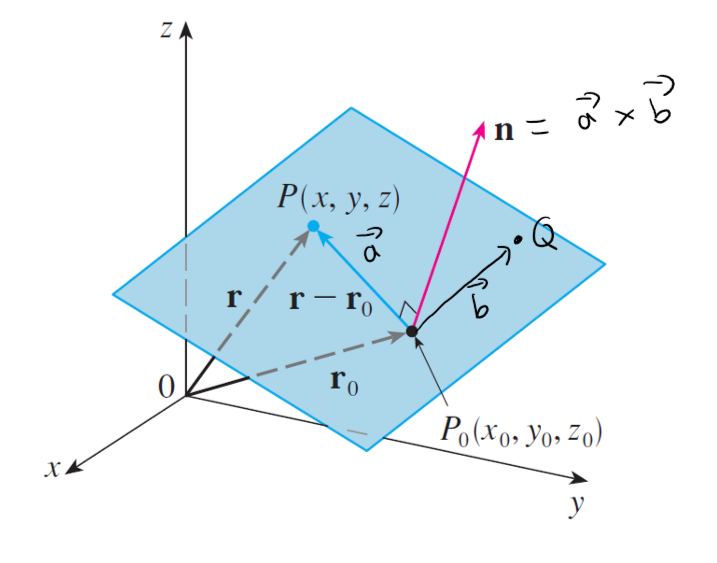
Question 12

How do you find the angle between two intersecting planes?

Solution:

We can use the dot product of the normal (perpendicular) vectors of the two planes.

---

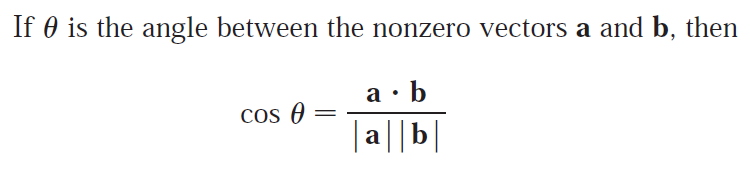
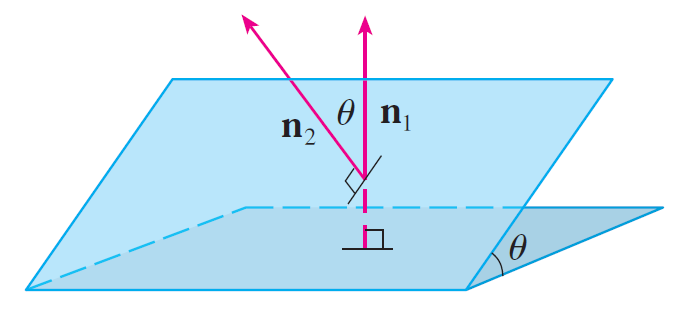
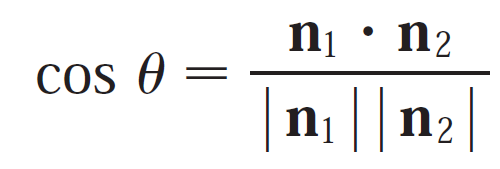
Question 13

Write a vector equation, parametric equations, and symmetric equations for a line.

Solution:

The vector, parametric, and symmetric equations of a line are shown.

---

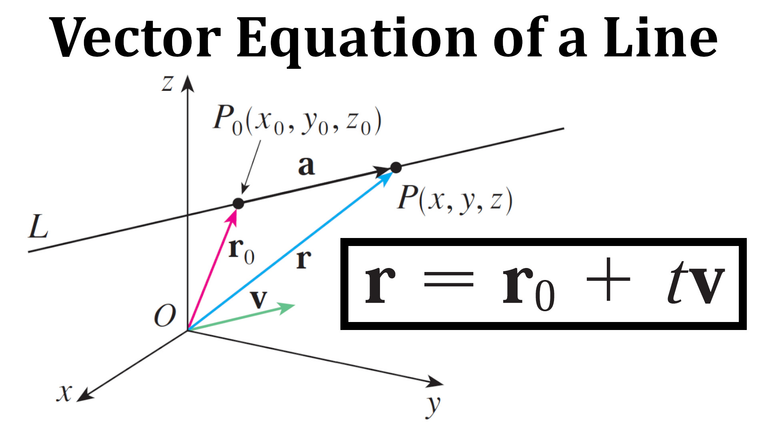
Question 14

Write a vector equation and a scalar equation for a plane.

Solution:

The vector and scalar equations of a plane are shown.

---

Question 15

(a) How do you tell if two vectors are parallel?

(b) How do you tell if two vectors are perpendicular?

(c) How do you tell if two planes are parallel?

Solution to (a):

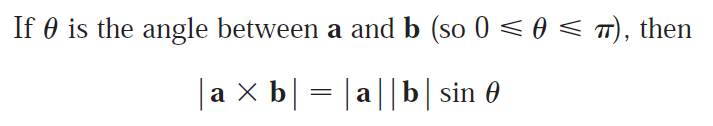
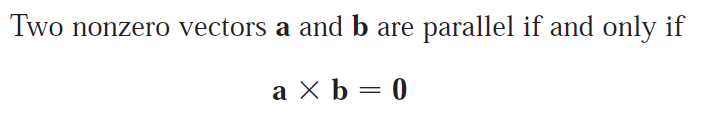
If two vectors are parallel then the angle between them is zero, thus the cross product is zero since sin(0°) = 0.

Solution to (b):

If two vectors are perpendicular, then their dot product is zero (since cos(90°) = 0).

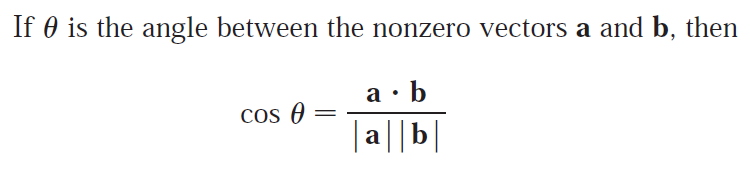
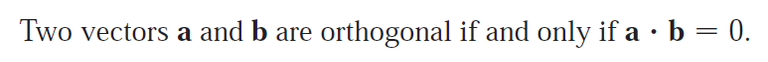
Solution to (c):

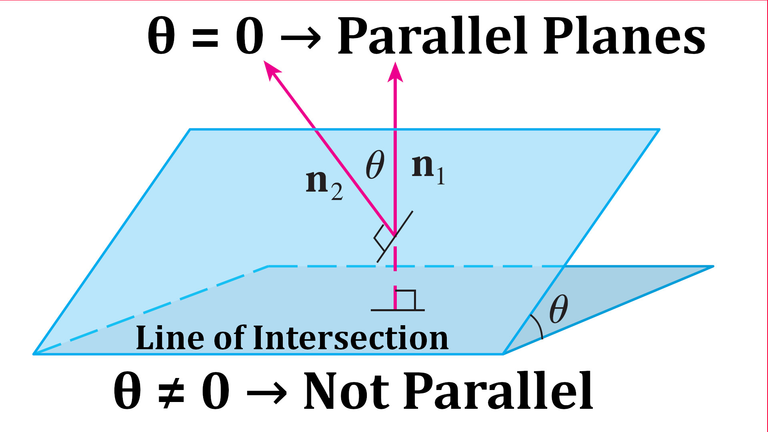
If two planes are parallel then the angle of their intersection (between their normal vectors) is zero, which can be determined using the dot product.

---

Question 16

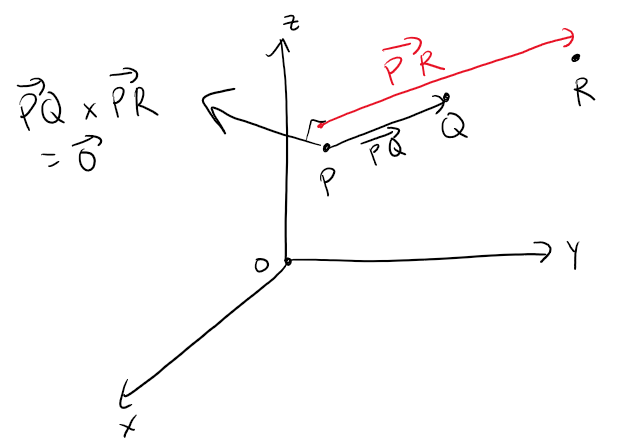
(a) Describe a method for determining whether three points P, Q, and R lie on the same line.

(b) Describe a method for determining whether four points P, Q, R, and S lie in the same plane.

Solution to (a): 3 Points on a Line

To determine whether three points lie on the same line, we can take the cross product of the position vectors PQ and PR.

If the cross product is zero, then the position vectors are parallel, hence the points P, Q, R lie on the same line.

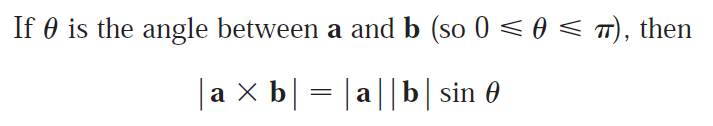
Solution to B: 4 Points on a Plane

To determine whether four points lie on the same plane, we can compute the scalar triple product of the position vectors PQ, PR, and PS.

If the scalar triple product is zero, then the volume of the parallelepiped is zero, thus all the points are on the same plane.

---

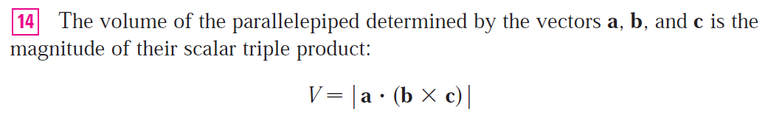
Question 17: Distances between Points, Lines, Planes

(a) How do you find the distance from a point to a line?
(b) How do you find the distance from a point to a plane?
(c) How do you find the distance between two lines?

Solution to (a): Distance from a Point to a Line

To determine the distance from a point to a line, we can use the fact that the magnitude of the cross product is the area of a parallelogram, where the height is the distance from a point to the base (which is a just a line).

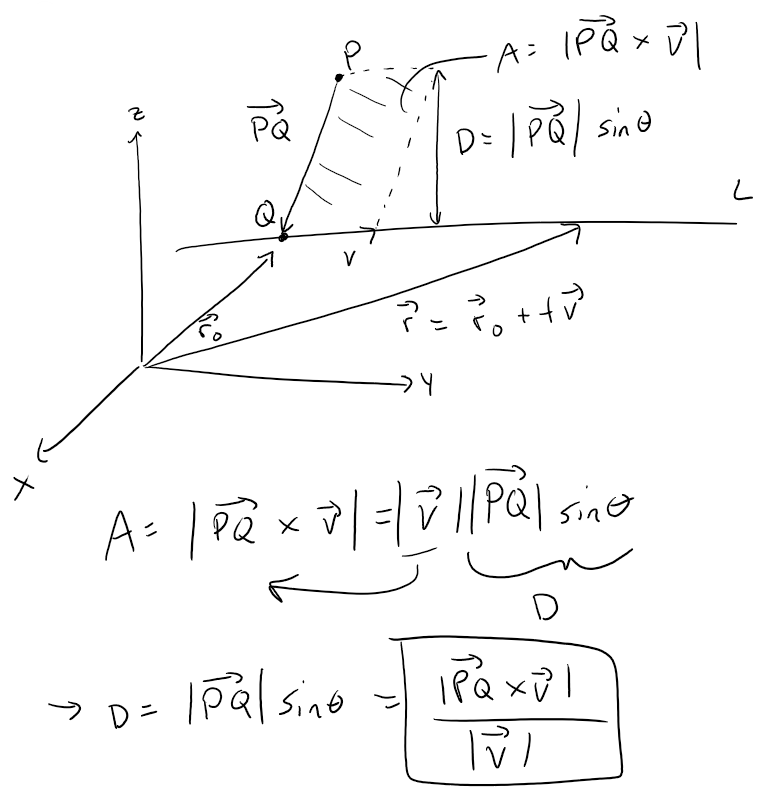
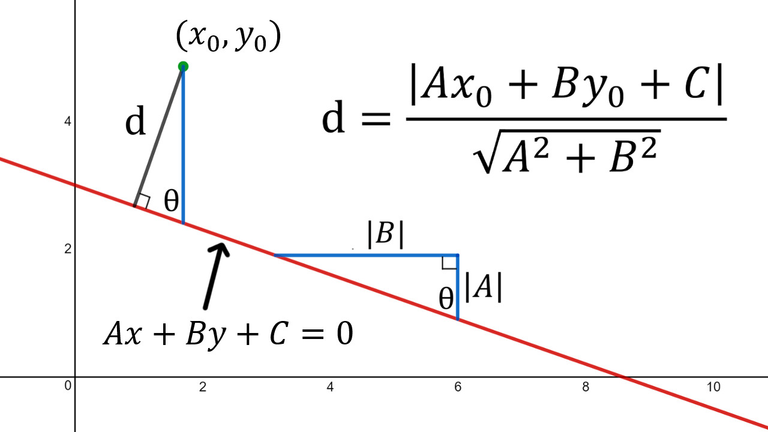
Note that in 2D, we can use the following equation:

Solution to (b): Distance from a Point to a Plane

The distance from a point to a plane can be calculated by the equation below.

Solution to (c): Distance between Two Lines

If two lines intersect, then the shortest distance is zero at the point of intersection; we can equate both lines and solve for their parameters.

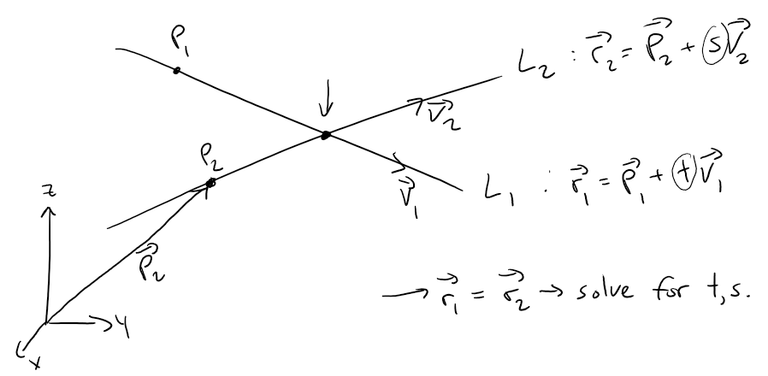
If there is no solution, then the lines don't intersect.

If two lines are parallel then the cross product of their position vectors is zero (because sin(0°) = 0), and we can solve the distance by the same method as with the distance between a point and a line.

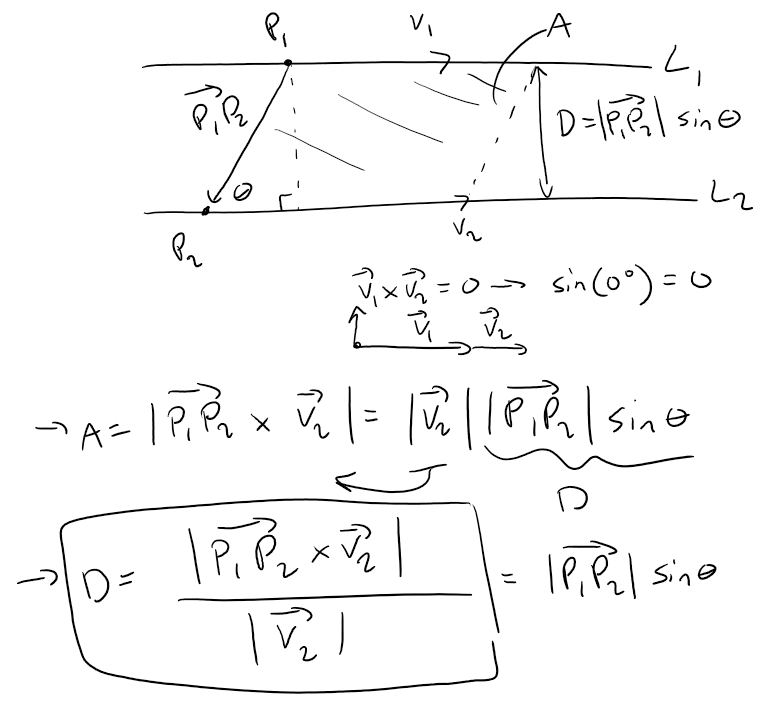
If two lines don't intersect and are not parallel, then they are skew lines.

Skew lines can be viewed as being on two parallel planes: https://www.geogebra.org/calculator/kccatfbp

This means we can just use the distance between a point and a plane formula by first obtaining the normal vector of the two direction vectors via the cross product.

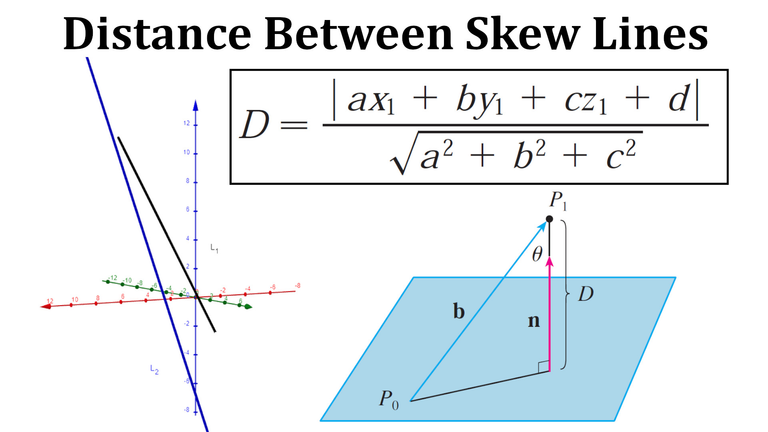
The distance formula is just the scalar projection of a vector connecting the two lines unto the normal vector.

---

Question 18

What are the traces of a surface?

How do you find them?

Solution:

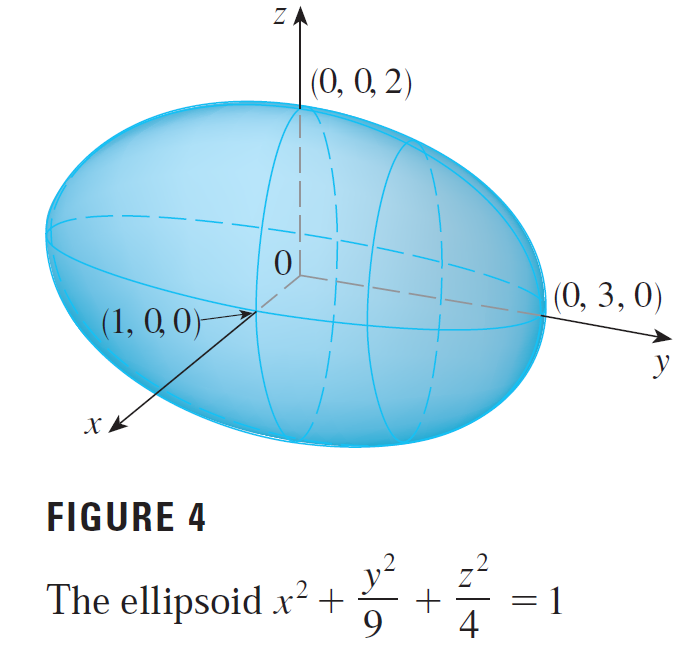
Traces are the curves of intersection of a surface with planes parallel to the coordinate planes.

We can find traces by setting the x, y, or z coordinate to a constant k.

For example, an ellipsoid is a surface with vertical and horizontal traces being ellipses.

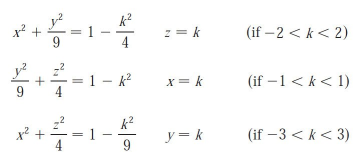
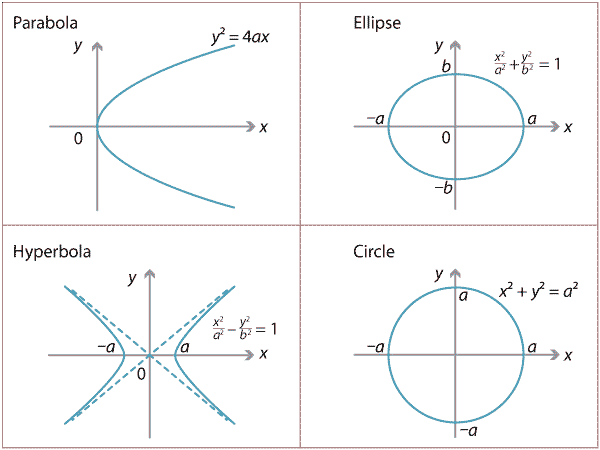
Recall the equations of parabolas, ellipses, hyperbolas, and circles.

---

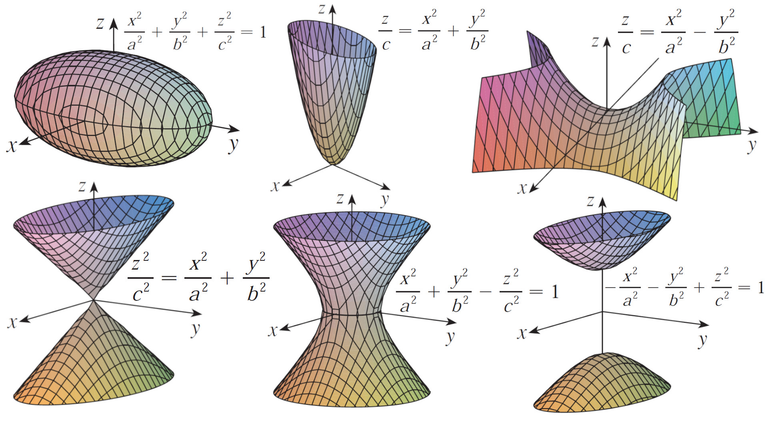
Question 19: Formulas of 6 Quadric Surfaces

Write equations in standard form of the six types of quadric surfaces.

Solution:

The equations in standard form of the six types of quadric surfaces are listed below.

Ellipsoid

Cone

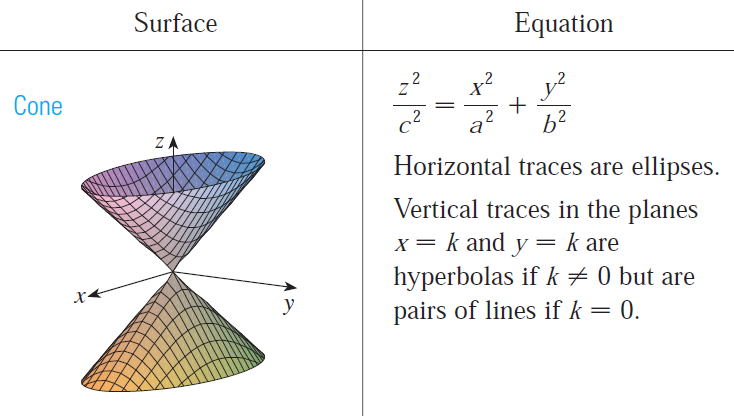
Elliptic Paraboloid

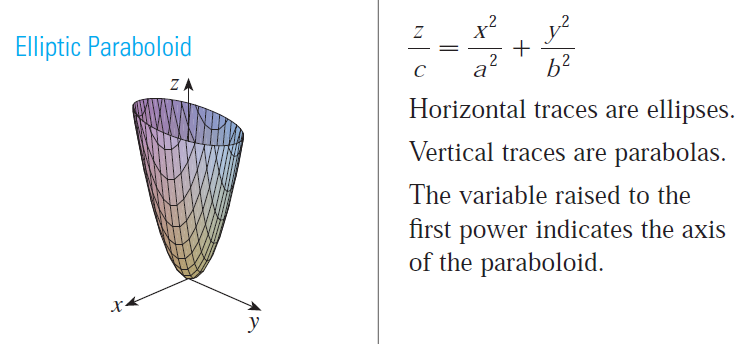
Hyperboloid of One Sheet

Hyperbolic Paraboloid

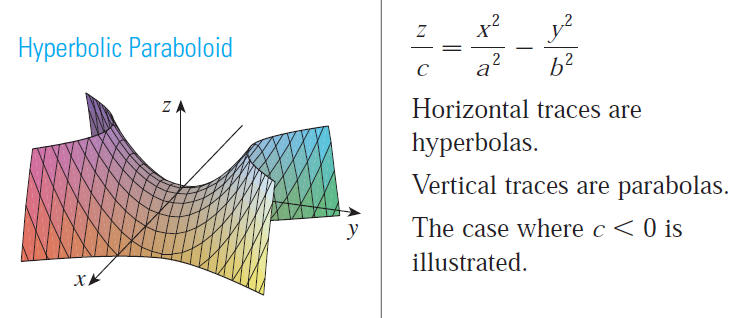
Hyperboloid of Two Sheets

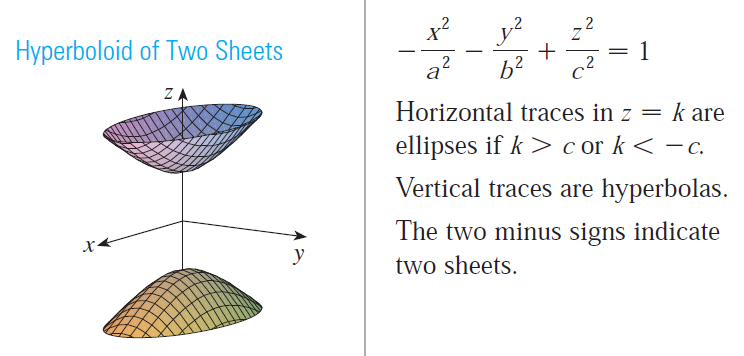
Summary