Situation:

Once upon a time, on a way through the old wild mountainous west,…
… a man was given directions to go from one point to another. The directions were "NORTH", "SOUTH", "WEST", "EAST". Clearly "NORTH" and "SOUTH" are opposite, "WEST" and "EAST" too.
Going to one direction and coming back the opposite direction right away is a needless effort. Since this is the wild west, with dreadful weather and not much water, it's important to save yourself some energy, otherwise you might die of thirst!

How I crossed a mountainous desert the smart way:

The directions given to the man are, for example, the following:
["NORTH", "SOUTH", "SOUTH", "EAST", "WEST", "NORTH", "WEST"].

You can immediately see that going "NORTH" and immediately "SOUTH" is not reasonable, better stay to the same place! So the task is to give to the man a simplified version of the plan. A better plan in this case is simply:
["WEST"]

Other examples:

In ["NORTH", "SOUTH", "EAST", "WEST"], the direction "NORTH" + "SOUTH" is going north and coming back right away.

The path becomes ["EAST", "WEST"], now "EAST" and "WEST" annihilate each other, therefore, the final result is [].

In ["NORTH", "EAST", "WEST", "SOUTH", "WEST", "WEST"] , "NORTH" and "SOUTH" are not directly opposite but they become directly opposite after the reduction of "EAST" and "WEST" so the whole path is reducible to
["WEST", "WEST"].

Task:

Write a function dirReduc which will take an array of strings and returns an array of strings with the needless directions removed (W<->E or S<->N side by side).

Notes:

Not all paths can be made simpler. The path ["NORTH", "WEST", "SOUTH", "EAST"] is not reducible. "NORTH" and "WEST", "WEST" and "SOUTH", "SOUTH" and "EAST" are not directly opposite of each other and can't become such. Hence the result path is itself : ["NORTH", "WEST", "SOUTH", "EAST"].

My problem with this kata [Mi problema con este kata]

The previous statement has a logic problem, since it asks you to simplify the way for the good man but, as we see in this last example, there is no such simplification. If we make the path we see that the man ends up just where he began, wasting energy and effort for nothing. This doesn't affect the problem solving at all, it is just an appreciation, but if we would really want to simplify the way for the good man, the solution would be different. Anyway, at the end of this post I will be proposing a solution to really simplify the path.

El enunciado anterior tiene un problema de lógica, y es que te pide que le simplifiques el camino al buen hombre pero, como vemos en este último ejemplo, no hay simplificación alguna. Si realizamos el recorrido vemos que el hombre termina justo dónde comenzó, gastando energía y esfuerzo en vano. Esto no afecta en lo absoluto a la resolución del problema, simplemente es una apreciación, pero si quisiéramos de verdad simplificarle el camino al buen hombre, la solución sería diferente. De todas formas, al final de este post estaré ofreciendo una solución para simplificar el camino de verdad.

In the comments of the exercise there were certain discussions in this regard, from other users who, like me, were confused about this statement. While it is true that this point is clarified in the explanation of the exercise, the point that user lotheravanti presents doesn't cease to be curious:

En los comentarios del ejercicio hubo ciertas discusiones al respecto, de otros usuarios que, como a mí, les pareció confuso dicho enunciado. Si bien es cierto que en la explicación del ejercicio se aclara este punto, no deja de ser curioso el punto que el usuario lotheravanti plantea:

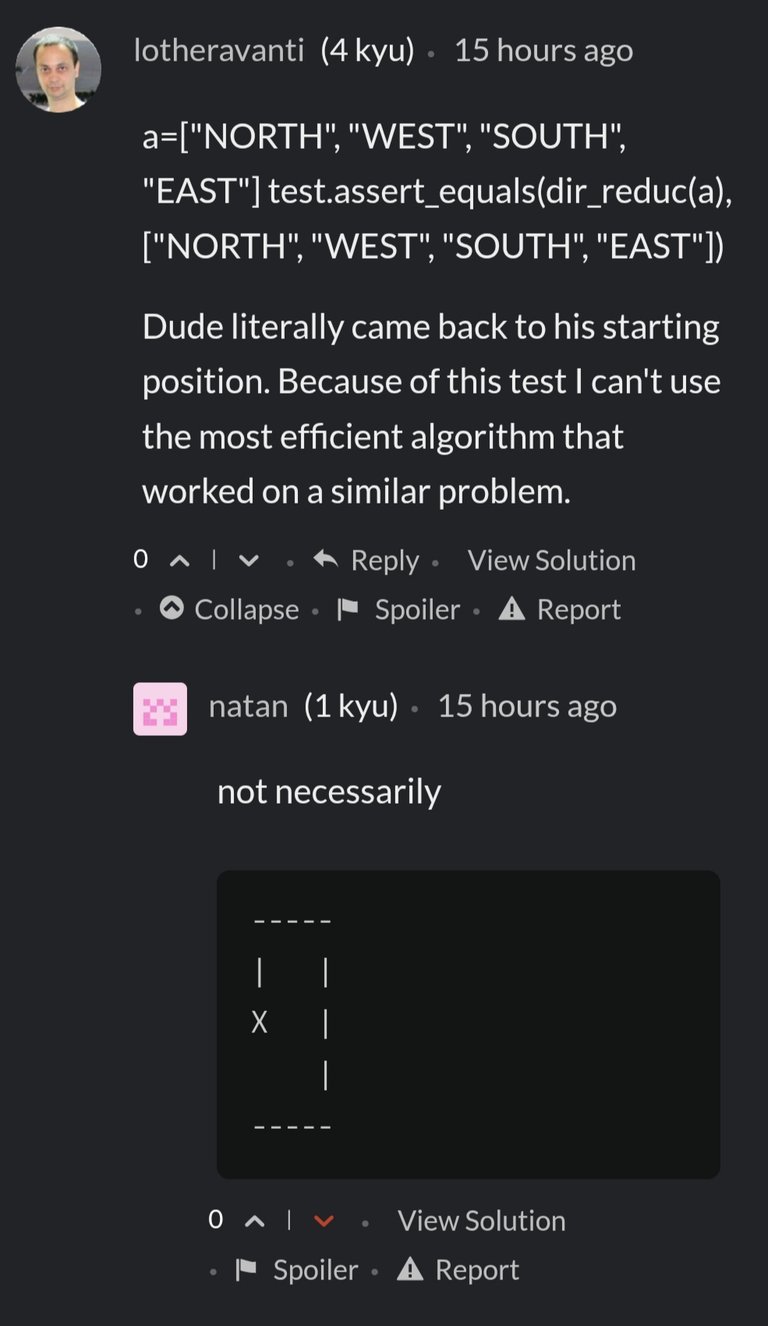
User natan tries to justify the explanation of the exercise with this example but, if so, it would continue wasting energy for nothing, because we could simply choose to go "SOUTH" and save us having to go all the way around. It also makes no sense, because then that would also apply to opposites that are directly next to each other. But we could take part of his argument to improve the statement of the exercise and justify, at least, how is different ["North", "South", "East", "West"] from ["North", "East", "South", "West"]. The statement could say: "..."the opposites that are directly next to each other" means the man go over the same distance in both directions (which is why traveling "NORTH" and immediately going "SOUTH" is an unnecessary waste of energy), and "the opposites that are separated" means the man is traveling different distances, that is why they are not directly canceled...". This possible explanation would still have its cons, but it would be a much better explanation than the initial one.

El usuario natan intenta justificar la explicación del ejercicio con este ejemplo pero, de ser así, se seguiría gastando energía en vano, pues podríamos optar por ir simplemente "SOUTH" y ahorrarnos toda la vuelta. Además no tiene ningún sentido, porque entonces eso también se aplicaría a los opuestos que están directamente uno al lado del otro. Pero podríamos tomar parte de su argumentación para mejorar el enunciado del ejercicio y justificar, al menos, por qué razón se diferencia ["North", "South", "East", "West"] de ["North", "East", "South", "West"]. El enunciado del ejercicio podría decir: "...los opuestos que están directamente uno al lado del otro recorren la misma distancia (es por eso que recorrer "NORTH" e inmediatamente "SOUTH" es un gasto de energía innecesario), y los opuestos que están separados recorren distancias distintas, es por eso que no son directamente cancelables...". Esta posible explicación aún tendría sus agujeros, pero sería bastante mejor que la explicación inicial.

A little more of the same here.

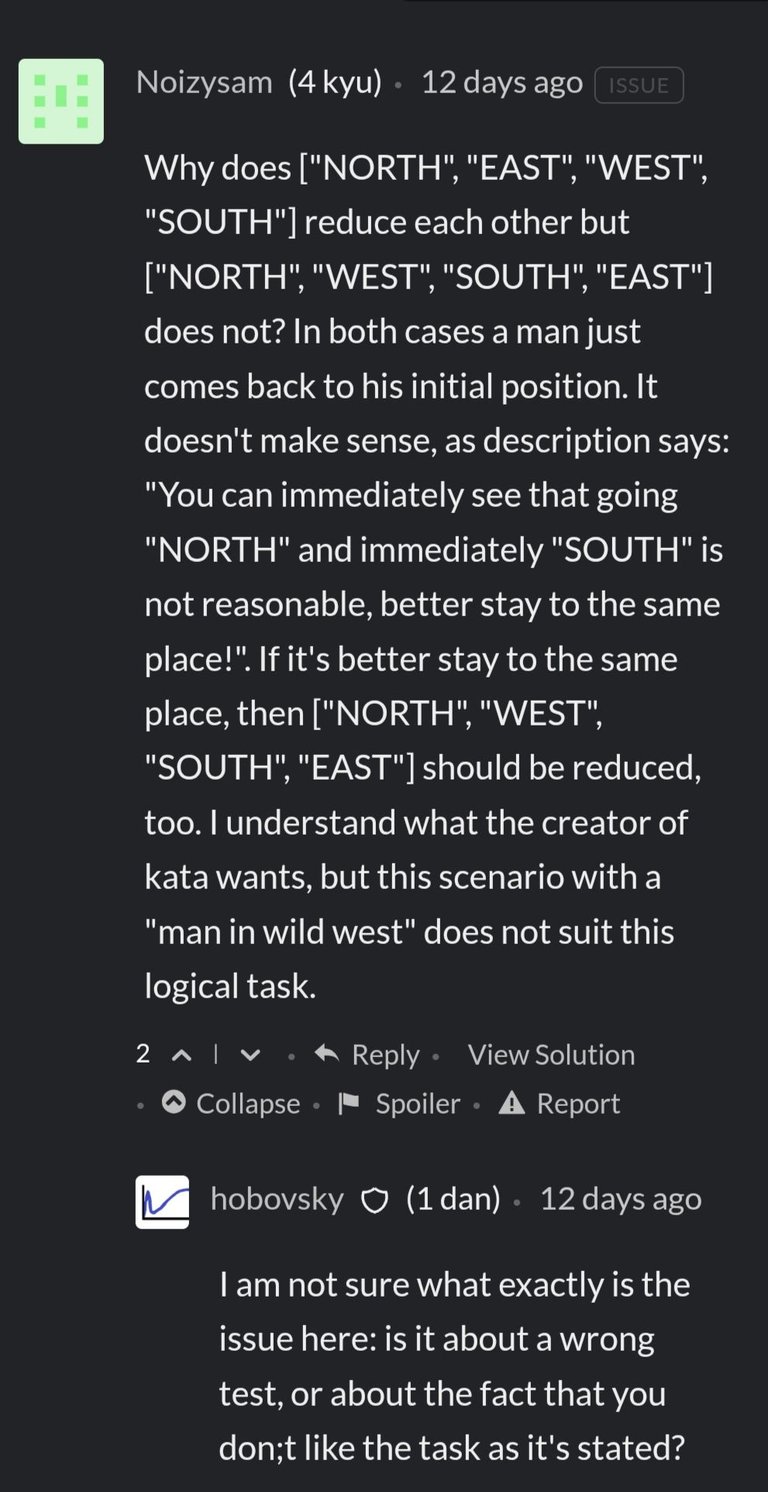
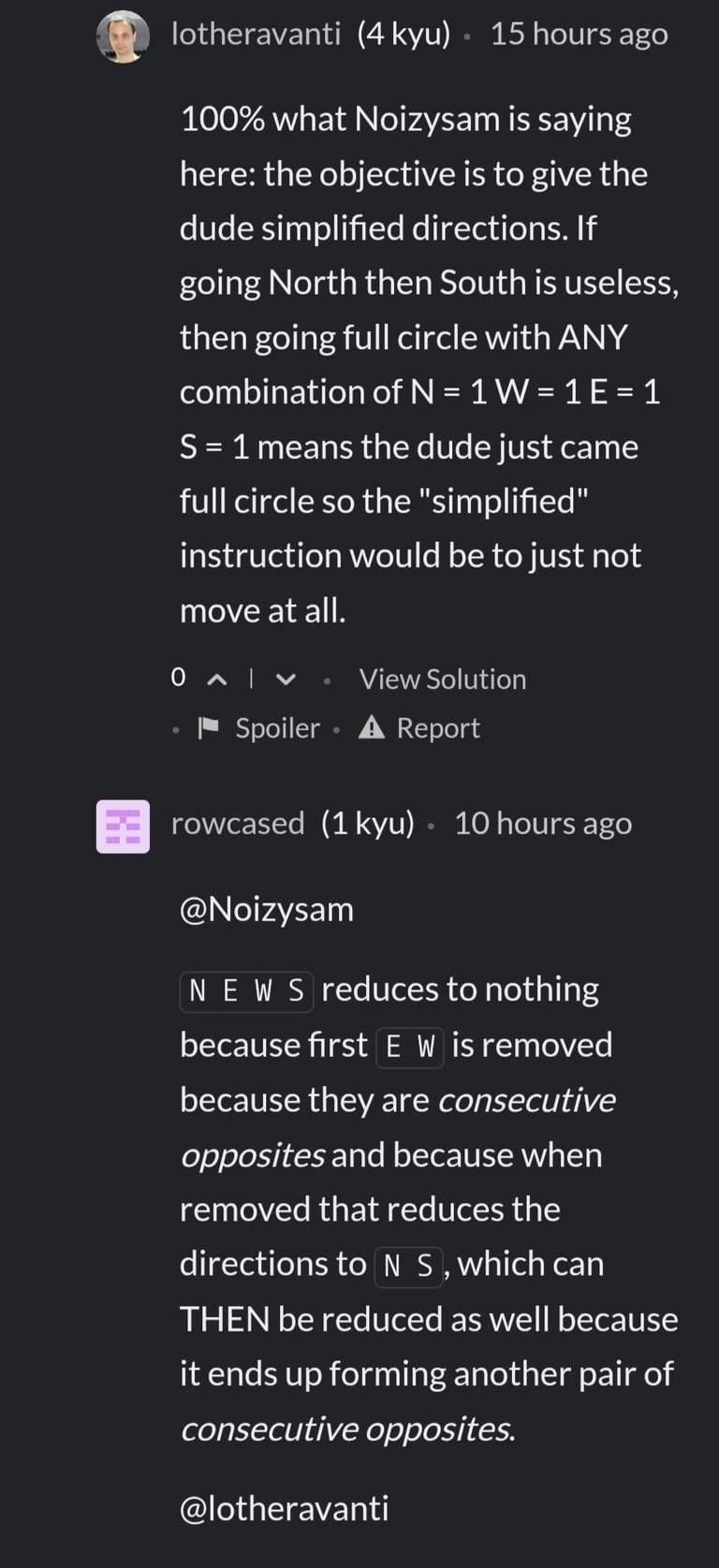
Un poco más de lo mismo por aquí.

It is assumed that any combination of "NORTH", "SOUTH", "EAST", "WEST" would mean returning to the same place and, therefore, making an unnecessary waste of energy. What user rowcased doesn't seem to understand is that both, the users who complain and I, understand perfectly the statement of the exercise and that the point is not in this fact. In fact, the user Noizysam points it out in his writing: "...I understand what the creator of the kata wants, but this scenario with a "man in wild west" does not suit this logical task". The point of all this actually is in advising the author of the kata to improve the statement of his exercise and avoid future conflicts or disagreements.

Se supone que cualquier combinación de "NORTH", "SOUTH", "EAST", "WEST" significaría volver al mismo lugar y, por tanto, realizar un gasto innecesario de energía. Lo que el usuario rowcased no parece comprender es que tanto los usuarios que se quejan, como yo, entendemos perfectamente el enunciado del ejercicio y que la cuestión no pasa por allí. De hecho, el usuario Noizysam así lo refleja en su escrito: "...Comprendo lo que el creador del kata quiere, pero este escenario con un "hombre en el viejo oeste" no va con esta tarea lógica". La cuestión en realidad pasa por aconsejar al autor del kata para que mejore el enunciado de su ejercicio y evitar futuros conflictos o inconformidades.

Really simplifying the way [Simplificando el camino de verdad]

User lotheravanti in his complaint said: "...Because of this test I can't use the most efficient algorithm that worked on a similar problem". Although it is not possible for me to know what the idea that had gone through his head was, I have reasons to believe that it is the same that I'm going to expose, or at least similar. For example, in another message he said: "...If going North then South is useless, then going full circle with ANY combination of N = 1, W = 1, E = 1, S = 1 means the dude just came full circle so the "simplified" instruction would be to just not move at all". The idea is simply counting how much of each direction are there in the array and subtract it from its opposite, so that the opposites always end up canceling and the directions that are left form the simplified instruction. For example: let us suppose "NORTH" is repeated 3 times and "SOUTH" 5 times. To prevent man from traveling unnecessarily in directions that are opposed, those 3 "NORTH" would be canceled with 3 of those "SOUTH", thus having 2 "SOUTH" left and the path completely simplified.

El usuario lotheravanti en su queja decía: "...Por culpa de este test no puedo usar el algoritmo más eficiente que funciona en un problema similar". Aunque no me es posible saber cuál era la idea que le había pasado por la cabeza, tengo motivos para creer que es la misma, o al menos parecida, que la que vengo a exponer. Por ejemplo, en otro mensaje decía: "...Si ir North y luego South es inútil, entonces ir en círculos con cualquier combinación N = 1, W = 1, E = 1, S = 1 significa que el tipo dió toda la vuelta, por lo que la solución "simplificada" sería no moverse en lo absoluto". La idea es simplemente contar cuánto de cada dirección hay en el array y restarlo de su opuesto, de manera que los opuestos siempre terminen cancelándose y las direcciones que queden formen la instrucción simplificada. Por ejemplo: supongamos que se repite "NORTH" 3 veces y "SOUTH" 5 veces. Para evitar que el hombre tenga que dar viajes innecesarios en direcciones que son opuestas, esos 3 "NORTH" se cancelarían con 3 de esos 5 "SOUTH", quedando así 2 "SOUTH" disponibles y el camino completamente simplificado.

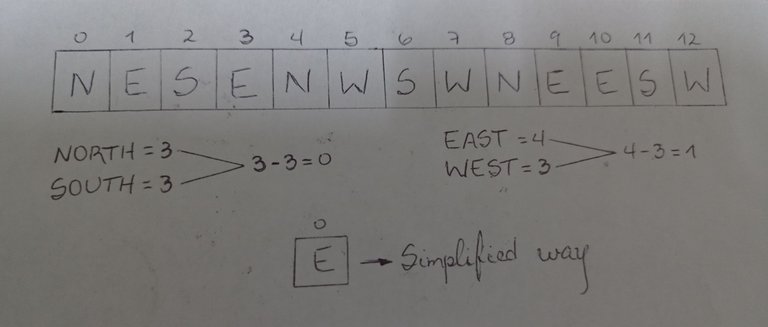
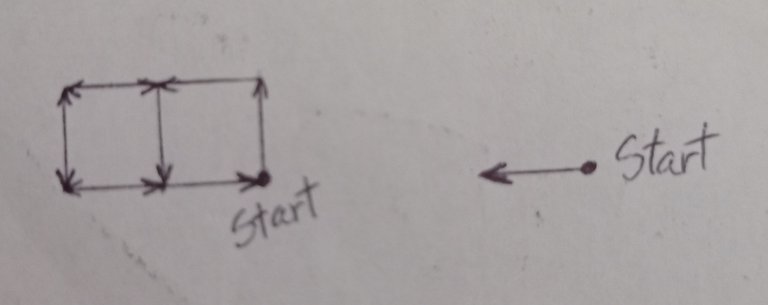
In this example we can see that none of the directions are "directly opposite" and, nonetheless, if we make the path we will see how stupid it is, since we are constantly going around without stopping until arriving (after having passed it so many times) to the place of destination. If the kata would allow us to simplify cases like this, we would really be making the good man's life easier on his way.

Therefore, the idea is in counting how many times each direction is repeated, subtract each one from its opposite and put the remaining directions in an array, and for this we will use the generic class Dictionary <T>.

En este ejemplo podemos ver que ninguna de las direcciones son "directamente opuestas" y, sin embargo, si hacemos el recorrido observaremos lo estúpido que se hace, ya que estamos constantemente dando vueltas sin parar hasta recaer (luego de haberlo pasado tantas veces) en el lugar de destino. Si el kata nos permitiera simplificar casos como este, de verdad estaríamos haciéndole la vida más fácil al buen hombre en su camino.

Por tanto, la idea pasa por contar cuántas veces se repite cada dirección, restar cada una de su opuesta y meter en un array las direcciones restantes, y para ello vamos a hacer uso de la clase genérica Dictionary<T>.

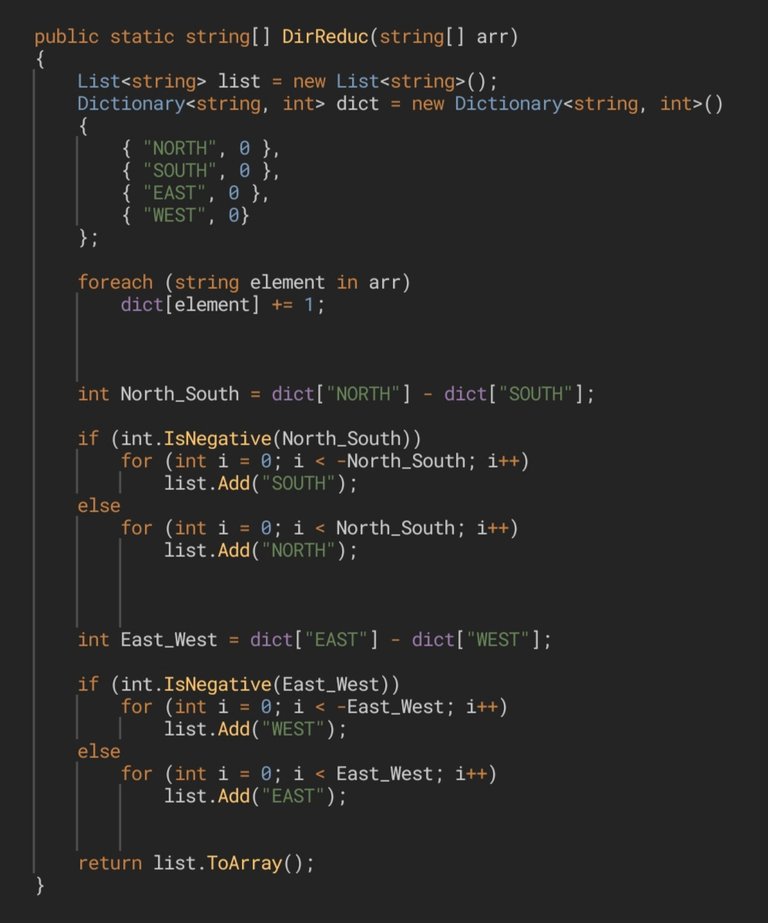
First we traverse the array to count the directions. A few lines before we have prepared a Dictionary<string, int>, whose key will be some of the directions and whose value will be the amount of each directions we find. Every time we find one, we look for the corresponding key in the dictionary and add 1 to its current value. Once we know the amount of every direction, we subtract the opposite directions and, depending on the result, we will add those that will form the simplified path to a list. To know which ones were left we will analyze the result of each subtraction: if they are positive, that means "NORTH" and "EAST" will have been left, and if they are negative, "SOUTH" and "WEST" then. Finally we turn the list into an array before returning it.

Primero recorremos el array para realizar el conteo de las direcciones. Unas líneas antes hemos preparado un Dictionary<string, int>, cuya clave será alguna de las direcciones y cuyo valor será la cantidad que encontremos de cada dirección. Cada vez que demos con una, buscamos en el diccionario la clave correspondiente y añadimos 1 a su valor actual. Una vez que conocemos todas las cantidades, restamos las direcciones que son opuestas y, en dependencia del resultado, vamos a añadir a una lista aquellas que conformarán el camino simplificado. Para saber cuáles quedaron analizaremos el resultado de cada resta: si son positivas habrán quedado "NORTH" y "EAST", y si son negativas habrán quedado "SOUTH" y "WEST". Finalmente convertimos la lista en array antes de devolverla.

I realized that it wasn't necessary to use dictionaries for this solution, I simply had to add 1 to a variable if the direction was "NORTH" or "EAST", or subtract 1 in case the directions were "SOUTH" or "WEST". Once this was done we would apply the same procedure as in the previous solution.

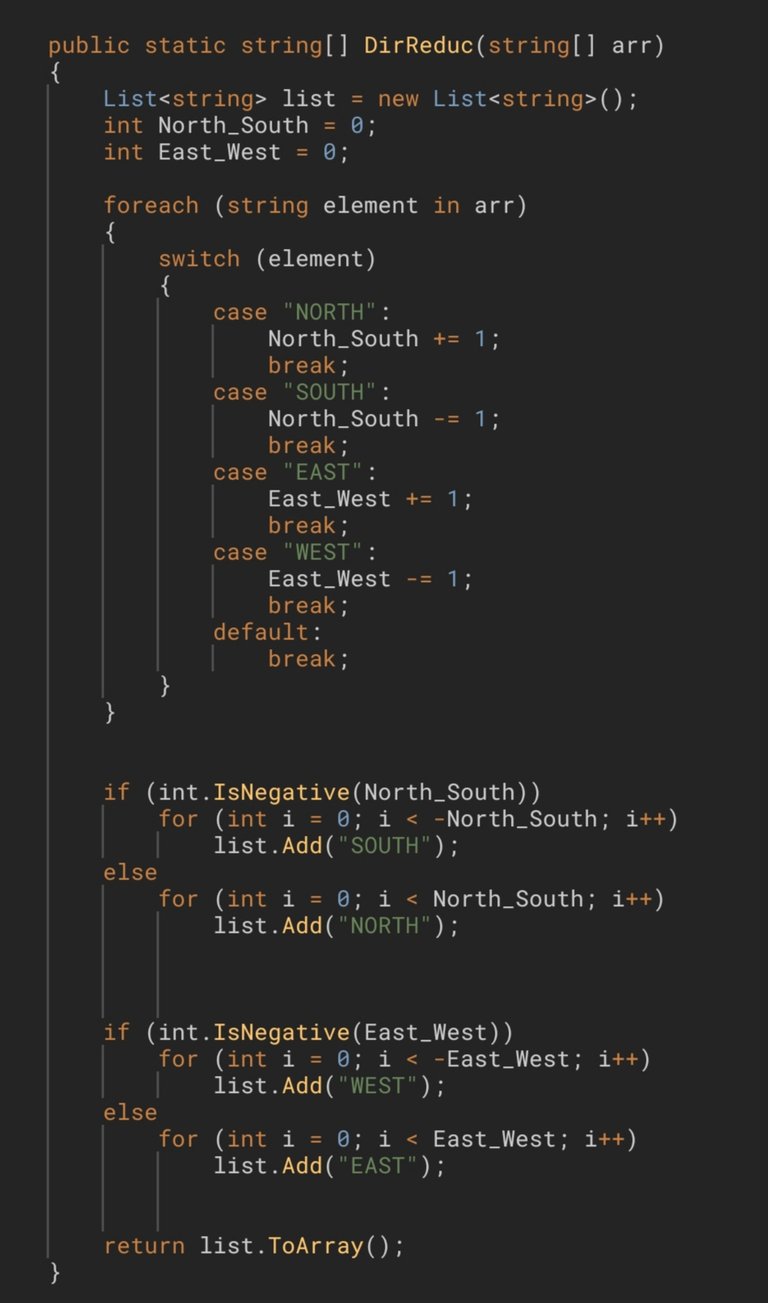
Me di cuenta de que no era necesario usar diccionarios para esta solución, simplemente tenía que añadir 1 a una variable si la dirección era "NORTH" o "EAST", o restar 1 en caso de que las direcciones fueran "SOUTH" o "WEST". Una vez hecho esto aplicaríamos el mismo procedimiento que en la solución anterior.

There is no need to say that if you know a better way to solve this you can write it in the comments, it will be really helpful. In the next post I will be analyzing my solution to the kata.

Está de más decir que si conocen una mejor manera de resolver esto pueden escribirla en los comentarios, me será de mucha ayuda. En el próximo post estaré analizando mi solución al kata.

---

English translation made with DeeplTranslate
Traducción al inglés hecha con DeeplTranslate