Hello everyone! Here we are again with this excercise from Code Wars platform, and today we will be analyzing a few other solutions proposed by another users.

Hola a todos! Aquí estamos de nuevo con este ejercicio de Code Wars, y estaremos analizando algunas de las soluciones propuestas por otros usuarios.

Alternatives solutions [Soluciones alternativas]

User SergeyFM proposes a solution almost the same as mine. The reason why I bring this solution is because it executes an unnecessary step. As we said in the previous post, we must find 2 numbers that are different, so we cannot add the same number twice. User SergeyFM understands this well, and that's why he establishes, as a second condition of his conditional block, that i must be different from j. However, there is a way to simplify this and avoid having to check the condition over and over again at each iteration. We simply initialize the control variable of the inner loop like this: int j = i + 1, and this way we make sure that both indexes will never match, which in other words means that we will never add the same number twice.

In the previous post we saw the proposal of user Acceptme3, and he always checked if the element in the index i was greater than target. This way he made sure that there was no number in the array whose sum with the current one resulted in target (since they were all positive), and he could jump to the next iteration of the loop. User SergeyFM also does the same thing, but in a different way. Instead of comparing them directly to see which of them is greater, he subtracts the current element of target and compares the result with 0. If it is less than 0 it won't be necessary to keep iterating (since we know that it will not store any negative number inside) and we can jump to the next iteration. The difference is that, while user Acceptme3 uses the keyword continue for this purpose, user SergeyFM includes this condition in his inner for loop. Both ideas are equivalent, since their purpose is that this loop is never executed under such a condition.

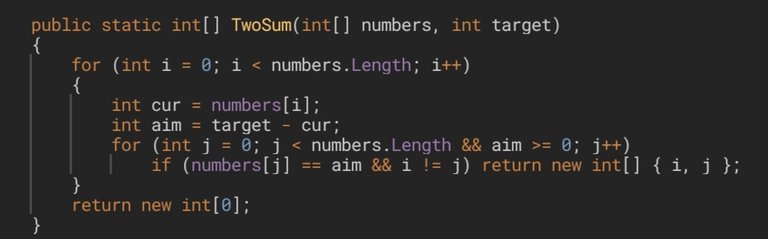
El usuario SergeyFM propone una solución prácticamente igual a la mía. La razón por la que traigo esta solución es porque ejecuta un paso innecesario. Cómo bien dijimos en el post anterior, debemos encontrar 2 números que sean diferentes, o sea que no podemos sumar el mismo número 2 veces. Esto el usuario SergeyFM lo entiende bien, y es por eso que establece como segunda condición de su bloque condicional que i sea diferente de j. Sin embargo, hay una manera de simplificar esto y evitar que se tenga que comprobar dicha condición una y otra vez a cada vuelta de bucle. Simplemente debemos inicializar la variable iteradora del bucle interior de esta forma: int j = i + 1, y así nos aseguramos de que ambos índices nunca van a coincidir, lo que en otras palabras significa que nunca vamos a sumar el mismo número 2 veces.

En el post anterior vimos la propuesta del usuario Acceptme3, y él comprobaba siempre que el elemento en el índice i fuera mayor que target. De esta manera se aseguraba que no existía ningún número en el array cuya suma con el elemento actual diera como resultado target (ya que todos eran positivos), y podía saltar a la siguiente iteración del bucle. El usuario SergeyFM también hace lo mismo, pero de una manera distinta. En lugar de compararlos directamente a ver cuál de los 2 es mayor, substrae el elemento actual de target y compara el resultado con 0. De ser menor que 0 no será necesario seguir recorriendo el array (pues sabemos que no almacenará ningún número negativo en su interior) y podremos saltar a la siguiente iteración. La diferencia es que, mientras el usuario Acceptme3 utiliza la palabra reservada continue para este propósito, el usuario SergeyFM incluye dicha condición en su bucle for interno. Ambas ideas son equivalentes, ya que su fin es que este bucle jamás se ejecute bajo dicha condición.

---

Solution using LINQ [Solución usando LINQ]

This solution is proposed by user LesRamer, and although it may seem very elegant since it uses LINQ and lambda expressions, the reality is that it is not very optimal, and we will see why. First it uses the Select() extension method and, for each element that is present in the array, it will create a new array with 2 elements, using the value of the current one and its respective index ((x, i)). The first value of this new array will be the index of the element. The second one will be obtained using the static method Array.IndexOf(). The overload that it uses in this case contains 3 parameters: the array where we are going to search, the value whose index we wanna find, and the place where we will start this searching. Let's translate this syntax to make it much more easy to understand: we are going to search in the array numbers the index of the element whose value is equal to target - x (being x the current one) and we will start searching from the element that follows the current one (i + 1). In other words, we will search for a value that added to the current number will result in the value we are asked for, and from it we will get the place it occupies in the array. The reason why we start searching from the current index plus one, is the same reason we had already explained in the previous examples, in order to not to add the same number twice. But this method doesn't end here, because we must extract one of all those arrays that we have created in order to return it, and that array will be the first of those whose second element is different from -1. The Array.IndexOf() method will not always find the element that we are looking for, and therefore it is necessary that it returns some value for those concrete cases: this value will be -1. Simplifying, of all those arrays we had created using Select(), we will choose the first one that fulfilled our condition: target - x.

This user acknowledges that his solution is far from optimal, in a comment in which he explains to another user the meaning of each part of his solution. In his own words:
"...Note that this implementation potentially constructs a lot of these two-element array that get thrown away. So, something like: target = 10, numbers = { 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 4, 6 } would redundantly search for a matching 10 for every 0 before finding the 4 & 6 elements at the end that sum 10. I didn't worry about this for this solution, but it would add to the challenge if the kata were turned into a performance optimization kata that took this idea to extremes".

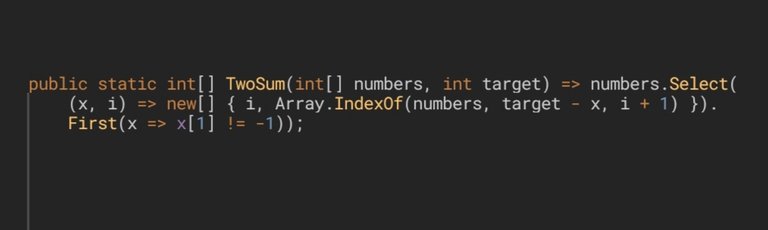
Esta solución es propuesta por el usuario LesRamer, y aunque pueda parecer muy elegante ya que usa LINQ y lambda expressions, la realidad es que no es muy óptima que digamos, y veremos el por qué. Primero utiliza el método de extensión Select(), con el que, por cada elemento que está presente en el array, creará un nuevo array con 2 elementos, utilizando el valor del elemento actual y su respectivo índice ((x, i)). El primer valor de este nuevo array será el índice del elemento. El segundo lo obtendrá utilizando el método estático Array.IndexOf(). La sobrecarga que utiliza en este caso contiene 3 parámetros: el array donde vamos a buscar, el valor al cual queremos hallarle su índice, y el índice a partir del cual comenzaremos a buscar. Traduzcamos esta sintaxis para que se entienda mucho mejor: vamos a buscar en el array numbers el índice de aquel elemento cuyo valor sea igual a target - x (siendo x el elemento actual) y comenzaremos dicha búsqueda a partir de aquel elemento que le sigue al actual (i + 1). En otras palabras, buscaremos un valor que sumado al número actual dará como resultado el valor que se nos pide, y de él obtendremos el lugar que ocupa en el array. La razón por la que comenzamos a buscar una casilla después del elemento actual, es la misma razón que ya habíamos explicado en los ejemplos anteriores, para no sumar el mismo número 2 veces. Pero el método no acaba aquí pues, de todos esos arrays que hemos creado, debemos extraer uno para devolverlo, y ese array será el primero de aquellos cuyo segundo elemento sea diferente de -1. El método Array.IndexOf() no siempre encontrará el elemento que buscamos, y por tanto es necesario que devuelva algún valor para esos casos concretos: dicho valor será -1. Simplificando, de todos los arrays que habíamos creado utilizando Select(), escogeremos el primero de aquellos que cumplieron con la condición: target - x.

El usuario reconoce que su solución no es para nada óptima, en un comentario en el que explica a otro usuario el significado de cada una de las partes de su solución. En sus propias palabras:
"...Ten en cuenta que esta implementación potencialmente construye un montón de estos arrays de 2 elementos que son desechados. Por tanto, algo como esto: target = 10, numbers = { 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 4, 6 } buscaría, de manera redundante, coincidir con target por cada uno de esos 0s antes de toparse con los elementos 4 y 6 que finalmente suman 10. No me preocupé acerca de esto para esta solución, pero hubiera sido más retador si el kata fuera de optimizar el rendimiento y llevara esta idea al extremo".

---

Another solution using LINQ [Otra solución que usa LINQ)

The last solution I am bringing today is proposed by the user Niksonman, who also uses LINQ and lambda expressions to solve the exercise. This method will return an array of 2 elements, as requested by the exercise. The first element of this array will be the index of the value that meets the condition u - t, target - x in other words. For this purpose it uses Array.IndexOf(), whose first parameter is the array of numbers, and, in order to find the second one, it calls the extension method Where(). This method will create an array with all those values that meet a certain condition (u - t) and then will choose the first one using the First() method. Array.IndexOf() will find the index of this value, and will assign it to the variable i. The second element of this array will be obtained by finding the index to the result of the expression u - n[ i ], using the variable i (of the first element) and the method Array.LastIndexOf().

We shouldn't worry about those cases in which Array.IndexOf() returns -1 since, as we have said, there will always be 2 values in the array whose sum is equal to target (or u in this case), so we will never get any IndexOutOfRangeException when finding n[i]. The reason for the optional parameter i is to avoid getting a compilation error: "i doesn't exist in the current context", although it could have been declared inside the method.

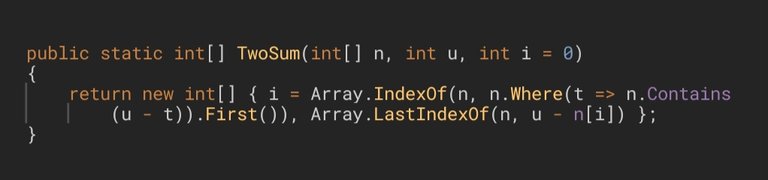
La última solución que les traigo es propuesta por el usuario Niksonman, que también utiliza LINQ y lambda expressions para resolver el ejercicio. Este método devolverá un array de 2 elementos, como nos pide el ejercicio. El primer elemento de este array será el índice de aquel valor que cumpla con la condición u - t, target - x en otras palabras. Para ello utiliza Array.IndexOf(), cuyo primer parámetro es el array de números, y para hallar el segundo recurrirá al método de extensión Where(). Este método va a crear un array con todos aquellos valores que cumplan cierta condición (u - t) y de todos ellos escogerá el primero utilizando el método First(). Este valor es al que Array.IndexOf() le hallará su índice, para luego asignárselo a la variable i. El segundo elemento de este array será obtenido hallándole el índice al resultado de la expresión u - n[i], utilizando la variable i (del primer elemento) y el método Array.LastIndexOf().

No debemos preocuparnos por aquellos casos en los que Array.IndexOf() devuelva -1 ya que, como hemos dicho, siempre existirán 2 valores en el array cuya suma sea igual a target (o a u en este caso), por lo que nunca incurriremos en ningún "IndexOutOfRangeException" al hallar n[i]. La razón del parámetro opcional i es para no incurrir en el error de compilación: "i doesn't exist in the current context", aunque bien se podría haber declarado en el interior del método.

---

English translation made with DeeplTranslate
Traducción al inglés hecha con DeeplTranslate