Una ecuación diofántica / A diophantine equation [ ES / EN ]
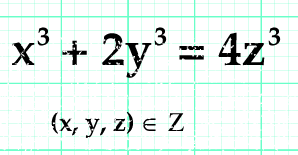
x³ + 2y³ = 4z³, (x, y, z) ∈ ℤ
| Español | English |
Solución:
( x, y, z ) = ( 0, 0, 0 ) |
|---|
Demostración:
Que ( 0, 0, 0 ) es solución resulta obvio, vamos a intentar encontrar otras posibles soluciones de la ecuación,
x ³ + 2y ³ = 4z ³ |
4z³ y 2y³, son ambos pares, lo que implica que x ha de ser par,
x1 = x / 2 8x1 ³ + 2y ³ = 4z ³ x1 ³ = ( 4z ³ - 2y ³ ) / 8 x1 ³ = 4(z / 2 ) ³ - 2( y / 2 ) ³ |
|
_\|/_ Este método de demostrar, por reducción al absurdo, la no existencia de soluciones, cada vez de menor valor, recibe el nombre de descenso infinito de Fermat |
|---|
Si ( x, y, z ) es solución, ( x/2, y/2, z/2 ) es solución también.
Reiterando este proceso, llegará un momento que encontraremos una raíz impar, lo cual es una contradicción, por lo tanto queda demostrada la no existencia de más raíces.
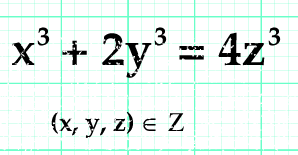
x³ + 2y³ = 4z³, (x, y, z) ∈ ℤ
| English | Español |
Answer:
( x, y, z ) = ( 0, 0, 0 ) |
|---|
Solution:
( 0, 0, 0 ) is a solution by inspection, we try to prove that is the only one solution,
x ³ + 2y ³ = 4z ³ |
4z³ y 2y³, are even, so x ought to be even also, if the equation has more solutions in integers,
x1 = x / 2 8x1 ³ + 2y ³ = 4z ³ x1 ³ = ( 4z ³ - 2y ³ ) / 8 x1 ³ = 4(z / 2 ) ³ - 2( y / 2 ) ³ |
|
_\|/_ This solution method, in which it is shown that any solution gives rise to a smaller solution, is known as the method of infinite descent |
|---|
if ( x, y, z ) is a solution, then so is ( x/2, y/2, z/2 ).
We could keep diminishing the solution as shown, and eventually arrive at a solution with an odd value, a contradiction.
Congratulations @j2e2xae! You have completed the following achievement on the Hive blockchain And have been rewarded with New badge(s)
Your next target is to reach 400 upvotes.
You can view your badges on your board and compare yourself to others in the Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPCheck out our last posts:
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.