Magnitudes Escalares y Vectoriales
Estamos nuevamente por acá compartiendo un nuevo tema con esta maravillosa comunidad, en esta ocasión estaremos desarrollando un tema muy importante para las ciencias, se trata de las magnitudes vectoriales y escalares.
Imagen realizada con la página web de diseño gráfico y composición de imágenes Canva.

Antes de comenzar a hablar de magnitudes escalares y vectoriales, es oportuno saber de qué se trata una magnitud. Una magnitud “es una propiedad de los cuerpos y elementos que permiten que sean medibles y, en algunos casos observables”. Es importante resaltar que las magnitudes pueden ser escalares o vectoriales.
Si hablamos sobre las magnitudes escalares, se puede decir que son aquellas que se pueden representar a través de una escala numérica en la que se distingue un grado de valor mayor o menor, según corresponda. Algunas de las magnitudes escalares son la temperatura, la energía, el tiempo, entre otras.
Por otra parte, tenemos las magnitudes vectoriales, que son aquellas que aportan mayor información sobre las propiedades de un cuerpo o elemento. Se dice, que las magnitudes vectoriales indican dirección o sentido que se pueden medir a través de un sistema de coordenadas; entre algunas de las magnitudes vectoriales se encuentran la velocidad, la fuerza, la aceleración, entre otras más.
Ahora bien, hablemos de los vectores y sus diversas aplicaciones en la cotidianidad, en la programación, el diseño digital, diseño gráfico y obviamente en las ciencias naturales. Su principal aplicabilidad se encuentra en la física, ya que permiten describir y analizar el movimiento de los objetos en el espacio. Por ejemplo, la fuerza ejercida sobre un objeto, donde la magnitud del vector corresponde a la intensidad de la fuerza, la dirección del vector indica la dirección en la que actúa la fuerza y el sentido del vector indica si la fuerza es atractiva o repulsiva.
En la ciencia, los vectores se utilizan en una amplia variedad de campos, como la ingeniería, la biología y la ecología. Entre algunas de sus utilidades están la representación de objetos en el espacio, la distribución de la energía en un sistema, la velocidad y dirección de las corrientes oceánicas, entre otras.
Ahora bien, ¿Qué es un vector? Básicamente, lo primero que podemos decir es que son flechas, que indican diferentes cantidades. Un vector posee diferentes características, la primera es la magnitud que se representa de la siguiente manera:
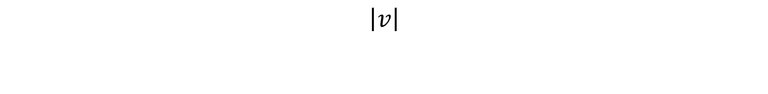
A la magnitud también se le conoce como modulo y, es lo que mide el vector.
Otras de las características de un vector son la dirección y el sentido. La dirección es la recta sobre la que se plantea el vector, la cual es continua e infinita en el espacio; mientras que el sentido está representado por la punta de la flecha que se expresa gráficamente, indicando el lugar hacia el cual se dirige el vector.
Para conocer un poco más sobre la dirección y el sentido del vector hay que observar el ángulo que se forma con respecto al eje x. Para conocer el sentido debemos estar atentos a la flecha de nuestro vector.
Ejemplo:
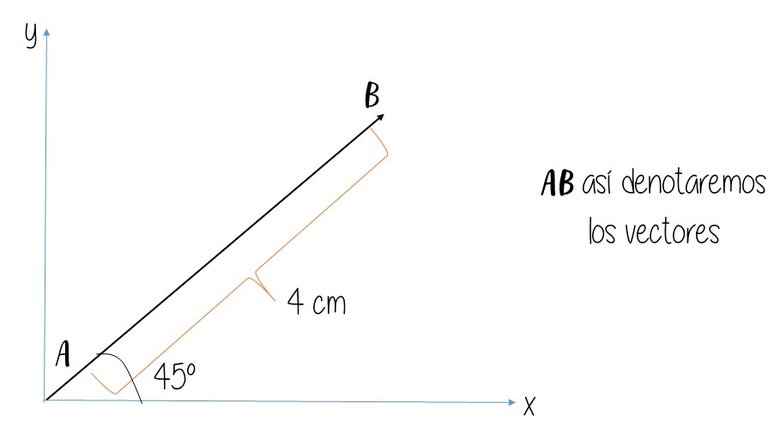
Si analizamos este vector, al cual llamaremos AB, el mismo tiene una magnitud o un módulo de 4cm, porque eso es lo que mide desde el origen hasta la flecha. La dirección es de 45° ya que ese es el ángulo que forma con respecto al eje x y su sentido es hacia donde apunta la flecha.
Primero que nada, es propicio recordar que
Magnitud = medida
Ya para despedirme espero que el tema sea del agrado de los lectores y deseo ver en los comentarios sus opiniones y aportes significativos que ayuden a la ampliación del tema y que genere un debate crítico y enriquecedor para la satisfactoria divulgación del conocimiento científico.

Ahora supongamos que tenemos dos vectores, como los que se representan a continuación:
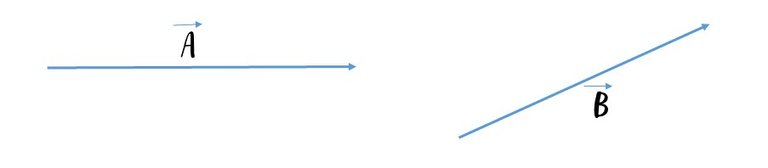
Si procedemos a medir cada vector con una regla podemos conocer su magnitud o modulo. Por ejemplo, el vector A mide 5 cm, mientras que el vector B mide 6 cm; sin embargo, cuando se habla de modulo se debe escribir de la siguiente manera:
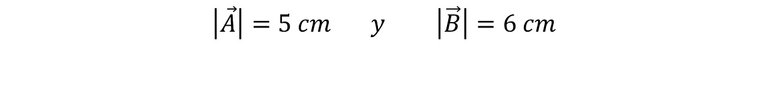
Esto se lee como la magnitud del vector A es de 5 centímetros o el vector A mide 5 centímetros. Para el segundo vector, podemos decir que la magnitud del vector Bes de 6 cm.
Ahora bien, veremos cómo determinar la magnitud o módulo de un vector usando sus componentes. Veamos los dos vectores que se presentan a continuación:
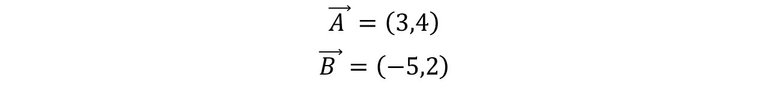
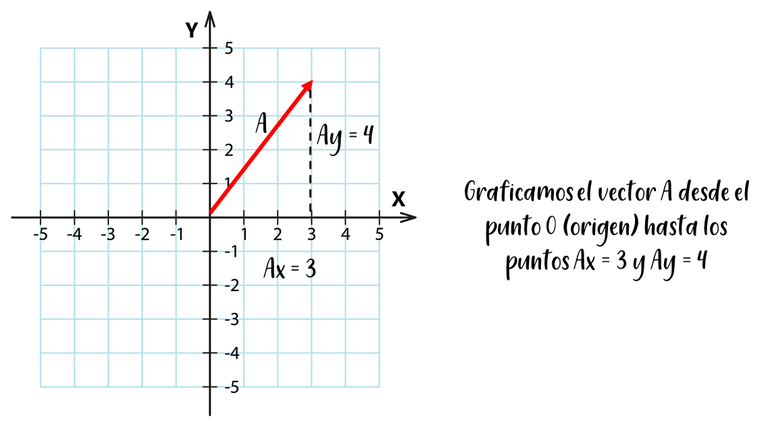
Como podemos ver las componentes del vector A son (3,4) y las del vector B (-5,2). Vamos a graficar el vector A en un sistema de coordenadas rectangulares.
Si observamos las componentes del vector, se puede evidenciar que se forma un triángulo rectángulo; por lo que, para determinar el modulo del vector utilizamos el “teorema de Pitágoras” ya que como es triángulo, el módulo es la hipotenusa del triángulo. En dicho teorema se cumple que: la suma de los cuadrados de las longitudes de sus catetos es igual al cuadrado de la longitud de la hipotenusa, entonces el módulo del vector seria de la siguiente manera:
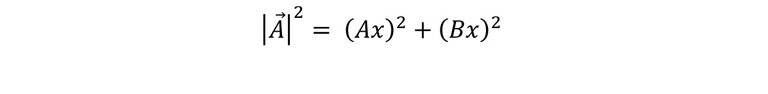
Sabemos que para despejar el módulo, es decir, quede elevado a la 1, se coloca una raíz cuadrada en ambos lados de la expresión.
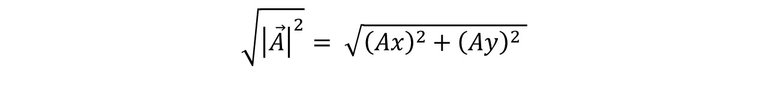
Se simplifica el cuadrado de la raíz y nos queda:
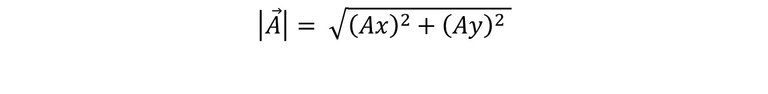
Sustituimos los valores dentro de la ecuación.
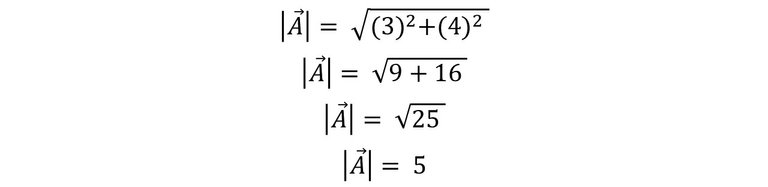
Quiere decir que el módulo del vector A es igual a 5. Suponiendo que las componentes están expresadas en centímetros, entonces el resultado es:
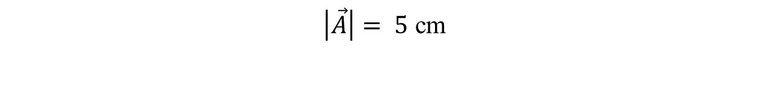
Si calculamos el modulo del vector B. Sabemos que sus componentes son (-5,2); es decir, Bx = -5 y By = 2; podemos sustituir los valore en la ecuación.
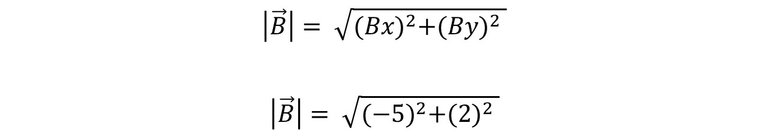
Recordemos que cuando en una potencia, la base es negativa y el exponente es par el resultado será positivo.
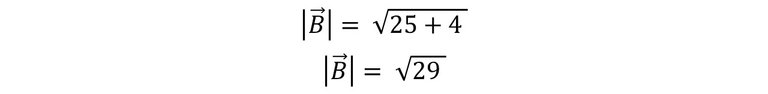
La raíz de 29 no es exacta, por lo que podemos sacarla en calculadora.
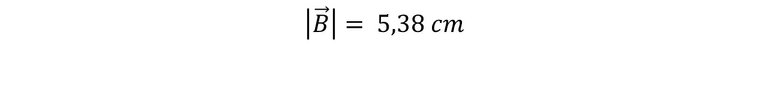
En conclusión, el módulo del vector B es de 5,38 centímetros.

Referencias
Baldor, A. (1941). Algebra. México, Publicaciones Cultural.
Hinds, J. (2002). Matemática 8. Caracas, Editorial Premier.



0
0
0.000
https://x.com/ILovePhysica/status/1786196790217183263
¡Felicitaciones!
Estás participando para optar a la mención especial que se efectuará el domingo 5 de mayo del 2024 a las 8:00 pm (hora de Venezuela), gracias a la cual el autor del artículo seleccionado recibirá la cantidad de 1 HIVE transferida a su cuenta.
¡También has recibido 1 ENTROKEN! El token del PROYECTO ENTROPÍA impulsado por la plataforma Steem-Engine.
1. Invierte en el PROYECTO ENTROPÍA y recibe ganancias semanalmente. Entra aquí para más información.
2. Contáctanos en Discord: https://discord.gg/hkCjFeb
3. Suscríbete a nuestra COMUNIDAD y apoya al trail de @Entropia y así podrás ganar recompensas de curación de forma automática. Entra aquí para más información sobre nuestro trail.
4. Visita nuestro canal de Youtube.
Atentamente
El equipo de curación del PROYECTO ENTROPÍA
Thanks for your contribution to the STEMsocial community. Feel free to join us on discord to get to know the rest of us!
Please consider delegating to the @stemsocial account (85% of the curation rewards are returned).
You may also include @stemsocial as a beneficiary of the rewards of this post to get a stronger support.